Cryptography Reference
In-Depth Information
One concept that we introduced in the addition formulation above is that we can add a point to itself, that is,
calculating
P
+ P. We could even add a point to itself multiple times, getting
P
+
P
+ P, and so forth. Since we
have no concept of multiplying points by each other, we can use the notation
n P
to mean “add
n P
's together”
(which is
n
- 1 addition operations), so that 0P = ∞, 1P = P, 2P =
P
+ P, 3P =
P
+
P
+ P, and so forth.
Taking a closer look at the previous example, you might note that
Q
= 2
P
, and therefore the result is
P
+ 2P
= 3P.
Some of our algorithms we will be developing later involve computing very large multiples of points. The
above construction doesn't seem to lend itself well to computing, say, 1048577P. It turns out we can use a short-
cut based on powers of two. Once we have computed
P
+
P
= 2P, we can easily calculate 2P + 2P = 4P. And
then, in a single additional operation, we have 4P + 4P = 8P, and so forth. Therefore, the trick is to take the
multiple that we want and to express it as a sum of powers of two. Once we have such a representation, we can
simply calculate each multiple of
P
that is a power of two and add them together. We can save even more time
by caching intermediate values.
Thus, in our above example, we can write 1,048,577 = 1,048,576 + 1 = 2
20
+ 2
0
, meaning that 1,048,577P =
(2
20
+ 2
0
)
P
= 2
20
P
+
P
. It takes 20 point-additions to calculate 2
20
P
, and one final one to add in the last P, for a
total of 21 additions. That's definitely a far cry less than adding
P
to itself 1,048,576 times.
2.6.2 Elliptic Curve Cryptography
Any operation, including cryptography, that can be performed on integers or any other type of number can also
be applied to points on an elliptic curve. There are two challenges to overcome: How do we represent inform-
ation as points on an elliptic curve, and how do we adapt our operations to be more tailored toward elliptic
curves?
To answer the first question, I take the following construction from Reference [13]. Assume that we have an
elliptic curve in a finite field (
p
, +, ×), represented by the equation y
2
= x
3
+
ax
+ b. First, we represent our
message as an integer
m
between greater than or equal to 0 and less than p/100. We will then try up to 100 points
on the elliptic curve to represent the message, starting with
j
= 0:
1. Let
x
j
= 100
m
+
j
.
2. Compute The value of
u
may end up being our
y
j
value, or help us to find one.
3. Check to see if
u
(p-1)/2
≡ 1 (mod
p
). If not, then go back to Step 1. If the above congruence is true, then
u
is a square in F
p
, so
y
j
≡ (mod
p
).
4. If
p
≡ 3 (mod 4), we can calculate a square root of
u
, and hence
y
j
, with
u
(p+1)/4
mod
p
.
5. Else if
p
≡ 5 (mod 8), then we can calculate the square root by calculating a
(p-1)/4
mod
p
. If this is +1,
then the square root is
y
j
≡
u
(p+3)/8
(mod
p
). Otherwise (if the calculated number is - 1), then
y
j
≡ 2
u
.
(4u)
(p-5)/8
(mod
p
)[2].
6.Elseif
p
≡1(mod8),thenwecancalculate asquarerootof
u
aswell,butitisquiteabitmoreinvolved.
Cohen [2] recommends using Shanks's algorithm [9], even though it is probabilistic. Shanks's algorithm
works as follows [2, 9]:
(a) Take
p
- 1 =
2
e
q,
by continually dividing
p
- 1 by 2 until we get a non-integer. The result imme-
diately before the non-integer is
q
, and the number of times we divided will be
e
.
(b) Compute
z
← u
q
mod
p
.
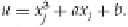

Search WWH ::

Custom Search