Cryptography Reference
In-Depth Information
we have 2, 5, and 10 taken out, as well any multiples (which then eliminates 4, 6, and 8, since they are multiples
of 2), giving us an RSR of
{1, 3, 7, 9}
There are many such RSRs. For example, if we multiply each number in an RSR by, say,
a
(with the con-
dition that
a
is relatively prime to
m
, so that they share no divisors), then the new numbers will also form an
RSR. This is because each number, which was already relatively prime to
m,
was multiplied by a number that is
relatively prime to
m
and hence will continue to be relatively prime (since the numbers won't grow new prime
factors).
We now have another important definition based on the RSR. The
Euler totient
(or just the
totient
) of a
number is the size of the RSR of the set of all integers less than it. In the previous example, we calculated the
Euler totient of 10. We typically write the totient of an integer
n
as
ϕ
(
n
). The previous example tells us that
ϕ
(10) = 4.
Another equivalent definition of the Euler totient of
n
is the number of positive integers less than
n
that are
relatively prime to
n
.
An important property of totients is called
Euler's totient theorem
(since Euler had many theorems). It
states that if
m >
1, and
a
and
m
are relatively prime, then
a
ϕ
(
m
)
≡ 1 (mod
m
).
To show how this is true, let's take a reduced set of residues, {
r
1
,
r
2
, ... ,
r
ϕ
(
m
)
} (since the totient is involved
withhowmanynumbersareinthisset).Thenwealsoknowthat{
ar
1
,
ar
2
,...,
ar
ϕ
(
m
)
}isareducedsetofresidues
(if the GCD of
a
and
m
is 1). Furthermore, we also know that for any number in the first set, there will be
exactly one number in the second set that is congruent to the first (since any two sets of reduced sets of residues
are equivalent modulo m), since every number that is relatively prime to
m
must be congruent to exactly one
number in each set.
Now consider the number a
ϕ(
m
)
×
r
1
×
r
2
× ... ×
r
ϕ(
m
)
. There is exactly one copy of
a
for each of the
r
's, thus
we can write this as
We also know that any set of RSRs is congruent modulo
m
, element by element, to any other set. This means
that we can replace the previous expression, so that our original number can be written
We also know that each
r
is relatively prime to
m,
meaning that we can divide by them, obtaining
This is exactly the result we wanted.
We have three corollaries to this statement. Specifically, since
we have to multiply both sides by
a
to obtain
Also, we can split off one of the
a
's from the former, to get
We can therefore see that a
ϕ
(
m
)-1
is the inverse of
a
(modulo
m
).
The other corollary might take a slight bit more convincing. If we have
x
≡
y
(mod
ϕ
(
m
)), then
g
x
≡
g
y
(mod
m
). Why? We know that, from the definition of a congruence,
x
=
y
+
k ϕ
(
m
). We can just rewrite
g
x
to get



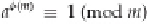


Search WWH ::

Custom Search