Cryptography Reference
In-Depth Information
a working knowledge of these topics in order to properly understand the workings of many cryptographic al-
gorithms (such as RSA) and cryptanalytic methods (such as factoring algorithms, like Pollard's Rho).
Before we dive in too deeply, let's go through a few quick definitions. The basic classes of numbers that we
are concerned with are integers, rational numbers, real numbers, and complex numbers.
Integers
( ) are the
class of numbers that we could theoretically count to, as well as zero and the negative of these counting num-
bers: {... , -3, -2, -1, 0, 1, 2, 3, ...}. These are positive and negative numbers with no fractional part, including
zero.
Rationalnumbers
( ), or just
rationals,
are the class of numbers that can be represented in the form p/q,
where
p
and
q
are both in , as with 1/2 or 2/3. Note that if
q
= 1, then the rational number is also an integer,
thus all integers are rational.
Real numbers
( ), or just the
reals,
include the integers and the rationals, as well
as any other numbers that can be numerically compared (less than, greater than) with integers and rationals, but
that may not have rational form, or even a finite representation. This includes numbers such as
π
, that, if
written out, would take an infinite number of digits to express their exact value. The real numbers that are not
rational are called, logically,
irrational.
However, the reals do not include numbers that have a component with
a square root of a negative number: These numbers cannot be compared with, say, the integer 2, to say which
one is “greater,” for example. The class of numbers that do include these are the
complex numbers
( ), which
all have the form
a
+
bi
, where
a
and
b
are in , and
i
=
2.2.1 Divisibility and Prime Numbers
We'll assume everyone understands what it means for an integer (say,
c
) to be
divisible
by another non-zero
integer (say,
a
). The definition we will use is that if
c
is
divisible
by
a,
then there exists another integer (say,
b
)
such that
c
=
a
×
b
. Hence, there is no remainder when
c
is divided by
b
or when
c
is divided by
a.
Although I
willtrytoavoidconfusingnotation,mathematicians oftendenotethefactthat
a
dividesinto
c
withnoremainder
by writing
a
| c, or
“a
divides
c.”
Now for a few properties of divisibility: It should come as no shock that division is transitive — that is, if
a
divides
c
and
c
divides another number (say,
e
), then
a
divides e. This can be easily shown by noting that
c
=
a
×
b
. And by our previous definition of divisibility, there must be a number
d
such that
e
=
c
×
d
. Then, by simple
substitution,
e
=
a
×
b
×
d
, which shows that
a
will divide into
e.
Another concept that is important is the
greatest common divisor
(GCD) of two numbers,
a
and
b,
often
written as a math function gcd(
a, b
). This number is defined to be the largest positive integer that divides both
a
and b. In the special case that the GCD of two numbers is 1, then these two numbers are called
relatively
prime.
If a number shares no common divisors with any numbers less than it, other than 1, then that number is
defined to be
prime.
2.2.2 Congruences
An important aspect of computers, which we will ultimately use to implement any cryptographic or cryptana-
lytic algorithm, is that they are
finite
;they do not contain unlimited memory, so we can't operate on
all
of the
integers, but smaller sets of them. We need to have some mathematics that understands this restriction. Luckily,
the theory of congruences allows us to perform operations on subsets of the integers. In fact, many of the mod-
ern crypto-algorithms actually rely on certain properties of congruences in order to perform their magic.
The basic definition of a
congruence
(although it is actually three definitions) is that if we have three in-
tegers,
a, b
, and m, then we say that
a
is
congruent
to b,
modulo
m, if
m
divides (a - b). This is written in the
more compact form,
a
≡
b
(mod m). We also refer to
m
as the
modulus.


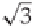

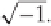
Search WWH ::

Custom Search