Cryptography Reference
In-Depth Information
To model these situations, it's often convenient to look at the situation in reverse; that is, rather than trying to
ascertain the probability that, say, of
n
people, there is at least one birthday collision, let's look at the probability
that there are
no
birthday collisions with
n
people.
In this case, we are going to assume that a person's birthday has a completely even chance of occurring on
any given day out of 365. We will generalize this to be any of
n
particular objects we might pick, so that this is
not specific to birthdays — it could be anything that someone has a finite number of choices for, such as cryp-
tographic keys. For birthdays, we just note that
n
= 365.
To reiterate, in this case we are interested in the probability of no repetition. For the first object, we will just
pick any object (in our birthday example, this is a day of the year), as we are guaranteed to have no repetitions;
thus, we can consider the probability of no repetition to be
n
choices out of
n
total choices, which is 1. The
second choice we make is slightly dependent on the first one. Since we picked one of the objects (or birthdays
in this case), we have
n
- 1 choices left in order for there to be no repetition, for which we have a probability of
(
n
- 1)/
n
. If we have a third person, then we have a probability of (
n
- 2)/
n
, since we now have two birthdays
that would cause a collision if chosen.
If we extrapolate this out to, say,
k
people, then this would be
Now, for every birthday we add on, we want there to be no repetitions. Thus, we start with one birthday, add
another (and calculate the probability), add another (and calculate the probability), and so on. In order to calcu-
late the likelihood of all of these events occurring in sequence, we
multiply
the probabilities together, since we
need the first one to happen, and then the second, and then the third, and so forth.
To look at it more simply, take fair coin tosses again. If we want to know the probability that we get heads
three times in a row, we take the probability that we have heads after the first throw (0.5); since we are already
in this situation with this probability, then the probability of both events happening is the probability of the first
times the probability of the second. Therefore, we multiply the first outcome by the probability that we have
heads the second time (0.5 × 0.5 = 0.25), and then multiply that by the probability that we have heads the third
time (0.25 × 0.5 = 0.125). Each successive event always leads to a multiplication of the previous probability
with the next.
For our probabilities in the birthday paradox above, we then have a probability of
Note that the leftmost
n
in the numerator cancels out one of the
n's
in the denominator. We can then pair each
number in the numerator with an
n
in the denominator, such as (
n
- 1)/
n
, which can be rewritten as 1 - (1/
n
),
with (
n
- 2)/
n
= 1 - (2/
n
), and so forth, to rewrite the product as
Here we have to use some calculus trickery to get this in a form more easily manipulatable. The concept of
Taylor polynomials allows us to use the approximation that
This approximation holds true when 1/
n
is very small, and therefore when when
n
is large. (Note that
e
is the
Euler constant, approximately equal to 2.71828.) For birthdays,
n
= 365 is perfectly sufficient for the approx-

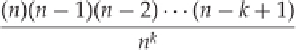


Search WWH ::

Custom Search