Cryptography Reference
In-Depth Information
If we learn that
A
j
= , then we know that
A
0
= =
E
(
P
, ); thus, we know that the encryption key is
possibly . However, it is not guaranteed to be that value; a reduction operator can produce false positives.
Also, we do not know the value of , since we threw away all but the final values of our above tables. This
means that in order to get our potential key, we must start at and regenerate the chain up to that point.
Since we take an average of
S
/2 operations to find the collision and
S
/2 operations to find the key, we take
S
operations in total.
5.2.3 Time-Space Trade-off Success
The success of this method in general relies on two values:
S
and
M
, the size of the table and the number of iter-
ations to perform, respectively. Obviously, if
S
and
M
are small, fewer keys will be covered in the intermediate
values of the ciphertext chains. For example, if
S = M = 2
25
, then a total of 2
50
keys are pre-computed in the
chains. If our key is a 64-bit value, then we have a 2
50
/2
64
= 2
-14
≈ 6.25 percent chance of finding a random key.
Clearly, then, we wish to have sizes that will yield good results. The optimal result is a guarantee (or as much
of one as we can obtain) that the key will be found using the above algorithm. This requirement essentially
means that
S
×
M
=
2
keysize
.
Hellman suggests in his original paper that the values be chosen so that if a key size
is
k
(i.e.,
2
k
total keys), then
S
will be 2
2k/3
and
M
will be 2
k/3
[7] This indicates final memory requirements of
2
k/3
. To compute the final time requirements for looking up a given key, we have a ciphertext list size of
2
k/3
.
Assuming that we can perform a lookup of a ciphertext in this list in inconsequential time, and an encryption/
reduction combination requires one computation step, then we can estimate that on average it will take
S
/2 to
find a value. With the above value of
S
, this means 2
2k/3-1
.
There are two consequences of using these values: The entire keyspace must be pre-computed, but the final
result allows us to perform a brute-force in two-thirds the time it would normally take. For example, using DES
(56-bit key, 64-bit block size), this would result in memory requirements of 2
56/3
× 56 bits or about 2.9 MB. The
average lookup time would be 2
56/3
or 2
37.33
operations (about 173 billion).
5.2.4 Flaws
One fundamental flaw of our system is the possibility of chain collision and convergence. Basically, if two
chains “collide,” where two of the intermediate values of two different chains are equal at some point, they will
converge and become the same chain after that point, owing to the deterministic nature of the chain iteration
function. This means significant redundant computations and storage.
Furthermore, the larger the table, the more likely we are to converge. At some point, the probability of a con-
vergence is so great that having a larger table actually will only decrease performance without providing any
additional benefits.
Another problem is
false positives
from the reduction function. In the above example with a 64-bit block size
and 60-bit key, there are 16 ciphertexts corresponding to the same key. This means we only have a 6.25 percent
chance of getting the correct key on the first try. Each false positive requires an additional ≈
S
/2 operations to
check the solution.
Finally, we also have the problem of loops. Our particular chain, through the reduction function, might find
itself in an infinite loop between some set of values. This would be equivalent to a self-convergence.
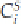




Search WWH ::

Custom Search