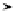Cryptography Reference
In-Depth Information
1
w
−
1
1
Figure 18.2 Parallelepiped centered at (
−
0
.
4
,
0
.
4) corresponding to lattice basis (3
,
2) and (2
,
1)
n
satisfies
method on input
w
∈ R
2
n
(9
/
2)
n/
2
)
w
−
v
≤
(1
+
w
−
u
for all
u
∈
L.
Proof
See Babai [
17
].
=
i
=
1
m
i
b
i
where
1
/
2.
In other words,
v
lies in the parallelepiped, centered at
w
, defined by the basis vectors.
Since the volume of the parallelepiped is equal to the volume of the lattice, if
w
is not in
the lattice then there is exactly one lattice point in the parallelepiped. The geometry of the
parallelepiped determines whether or not an optimal solution to the CVP is found. Hence,
though the rounding method can be used with any basis for a lattice, the result depends on
the quality of the basis.
Babai rounding gives a lattice point
v
such that
w
−
v
|
m
i
|≤
2
.Let
w
Example 18.2.2
Let
b
1
=
(3
,
2) and
b
2
=
(2
,
1) generate the lattice
Z
=
−
−
=
(
0
.
4
,
0
.
4) so that the solution to CVP is (0
,
0). One can verify that (
0
.
4
,
0
.
4)
1
.
2
b
1
−
and so Babai rounding yields
b
1
−
2
b
2
=
−
1
,
0). Figure
18.2
shows the
parallelepiped centered at
w
corresponding to the basis. One can see that (
2
b
2
(
−
1
,
0) is the only
lattice point within that parallelepiped.
Exercise 18.2.3
Consider the vector
w
=
(
−
0
.
4
,
0
.
4) as in Example
18.2.2
again. Using
2
the basis
{
(1
,
0)
,
(0
,
1)
}
for
Z
use the Babai rounding method to find the closest lattice
2
to
w
. Draw the parallelepiped centered on
w
in this case.
vector in
Z
We stress that the rounding method is not the same as the nearest plane method. The
next example shows that the two methods can give different results.
Example 18.2.4
Consider the CVP instance in Example
18.1.11
.Wehave
141
40
b
1
+
241
120
b
2
+
3
20
b
3
.
w
=