Hyperelliptic curves - Mathematics of Public Key Cryptography - page 194

ι ( P 5 )

ι ( P 4 )

P 2

P 1

P 3

P 4

P 5

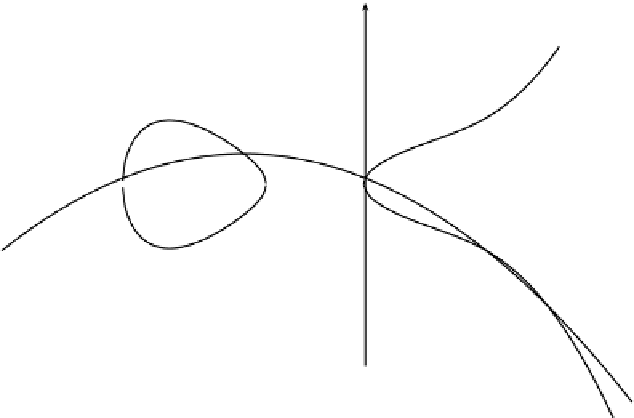
Figure 10.1 Cantor reduction on a hyperelliptic curve.

Lemma 10.3.17 Let D be an affine effective divisor on a hyperelliptic curve C with
Mumford representation ( u ( x ) ,v ( x )) . Define ( u † ( x ) ,v † ( x )) as in equation ( 10.10 ). Then
( u † ( x ) ,v † ( x )) is the Mumford representation of a semi-reduced divisor D † and D † ≡

D

2 .

on C ∩ A

Proof One checks that ( u † ( x ) ,v † ( x )) satisfies condition ( 10.5 ) and so there is an associated
semi-reduced divisor D † .
Write D = ( P 1 ) +···+ ( P n ) (where the same point can appear more than once).

− ∩ A

2

= +···+ + +···+

Then div( y ( P n + m ) for some points

P n + 1 ,...,P n + m (not necessarily distinct from the earlier n points, or from each other)
and

v ( x )) ( P 1 ) ( P n ) ( P n + 1 )

div( v ( x ) 2 + H ( x ) v ( x ) − F ( x )) ∩ A

2

= div(( y − v ( x ))( − y − H ( x ) − v ( x ))) ∩ A

2

=

( ι ( P n + m )). Now, div( u † ( x ))

( P 1 ) + ( ι ( P 1 )) +···+ ( P n + m ) + = ( P n + 1 ) + ( ι ( P n + 1 )) +···+

( ι ( P n + m )). It follows that D † = D † +

( P n + m ) + ( ι ( P n + 1 )) +···+ ( ι ( P n + m )) and that D =

2

div( u † ( x ))

2 .

div( y − v ( x )) ∩ A − ∩ A

Example 10.3.18 Consider
C : y 2 x 5 2 x 4 8 x 3 10 x 2

= = + − + + +

F ( x ) 40 x 1

over Q .Let P 1 = ( − 4 , 1) ,P 2 = ( − 2 , 5) ,P 3 = (0 , 1) and D = ( P 1 ) + ( P 2 ) + ( P 3 ). The

x 2

Mumford representation of D is ( u ( x ) ,v ( x )) = ( x ( x + 2)( x + 4) , − − 4 x + 1), which

is easily checked by noting that v ( x P i ) = y P i for 1 ≤ i ≤ 3.

monic ( v ( x ) 2 F ( x )) /u ( x ) =

To reduce D one sets u † ( x ) x 2 = − monic( − + 5 x −

2) and v † ( x ) v ( x )(mod u † ( x ))

6) = ( x − 3)( x − =− = 9 x − 7.

One can check that div( y − v ( x )) = ( P 1 ) + ( P 2 ) + ( P 3 ) + ( P 4 ) + ( P 5 ) where P 4 =

20), that div( u † ( x ))

(2 , − 11) and P 5 = (3 , − = ( P 4 ) + ( ι ( P 4 )) + ( P 5 ) + ( ι ( P 5 )) and that

div( u † ( x ) ,y v † ( x ))

2

D ≡ − ∩ A = ( ι ( P 4 )) + ( ι ( P 5 )). See Figure 10.1 for an illustration.