Biomedical Engineering Reference
In-Depth Information
dx
2
+ du
2
φ
dx
2
(π/2 - φ)
dx
1
+ du
1
dx
1
Fig. 2.10
Illustration for the geometric interpretation of the shearing strain
E
12
. The
left
and
right
illustrations of this figure represent the undeformed and deformed configurations, respectively.
The
heavy black lines
represent the same material filaments in the two configurations.
E
12
is equal
to one-half the change in angle that was originally a right angle between the
x
1
and
x
2
axes,
f
/2 in
this figure
thus it follows that (
e
1
þ
2
E
12
. Recalling the formula (A61) for
the dot product of two vectors, say
u
and
v
, as equal to the magnitude of the first times
the magnitude of the second times the cosine of the angle (say
Ee
1
)
(
e
2
þ
Ee
2
)
¼
z
) between them,
u
v
¼
u
i
v
i
¼j
u
jj
v
j
cos
z
, it follows that 2
E
12
¼j
e
1
þ
Ee
1
jj
e
2
þ
Ee
2
j
cos (
p
/2
f
),
where the angle (
p
/2
f
) is illustrated in Fig.
2.10
. The magnitude of
j
e
1
þ
Ee
1
j
is the square root of (
e
1
þ
Ee
1
)
(
e
1
þ
Ee
1
)
¼
e
1
e
1
þ
e
1
Ee
1
þ
e
1
Ee
1
þ
Ee
1
Ee
1
,
but since
e
1
e
1
¼
1and
Ee
1
Ee
1
is a higher order term, this reduces to the square root
of 1
2
E
11
, by a parallel of the arguments used above to obtain the formula for 2
E
12
.
At this point a classical approximation is used. This approximation is that 1
þ
þ e
2
may be neglected; the proof of this
approximation follows easily if one squares it. Then, since the square of
E
11
is a higher order term, the square root of 1
√
(1
þ
2
e
) if summands of the order
e
þ
2
E
11
is given by 1
þ
E
11
,thus2
E
12
¼
þ
E
11
)(1
þ
E
22
)cos(
p
f
) r
E
12
¼
þ
E
11
)(1
þ
E
22
)sin
f
(1
/2
(1
or
expanding; 2
E
12
¼
sin
f þ
(
E
11
þ
E
22
)sin
f þ
E
11
E
22
sin
f
. Finally, since the
angle
is small as are
E
11
and
E
22
, thus the neglect of higher order
terms gives 2
E
12
¼ f
, and the interpretation of
E
12
as one-half the change in an angle
that was originally a right angle between the
x
1
and
x
2
axes (Fig.
2.10
). These geometric
interpretations of the components of
E
as the change in the length of filaments, the
change in angles and the change in volume deformation between the undeformed
and the deformed configurations are the rationale for calling
E
the
strain
tensor.
f
is small, sin
f
Example 2.3.1
The deformation gradient and the inverse deformation gradient for the motion given
by (
2.12
) were computed in Example 2.1.4. Determine the restriction on the motion
given by (
2.12
) so the motion is infinitesimal. Find the strain tensor
E
and the
rotation tensor
Y
for the infinitesimal motion.






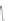

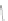
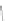
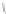




Search WWH ::

Custom Search