Cryptography Reference
In-Depth Information
Beispiel: n=5 (prim), die Elemente sind a,b
{0, 1, 2, 3, 4}
Um das multiplikativ inverse Element für a
0 zu finden, kann man die Folge der Produkte
1·a, 2·a, 3·a, … aufstellen. Sobald der Wert für ein Produkt (a·b) mod n = 1 auftritt, ist mit
b=a
1
das multiplikativ inverse Element a
1
zu a gefunden.
Die Folge 1·a, 2·a, 3·a, … kann man auch dadurch erzeugen, indem man, ausgehend von dem
Element a, jeweils den Wert a addiert, um von einem Folgen-Element zum Nachfolger-
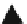
Element zu kommen. In Abb. 2-2 ist der Zyklus aller n=5 Restklassen modulo 5 als Kreis
dargestellt. Die Folge der Elemente 1·a, 2·a, 3·a, … ist für das Beispiel a=2 durch Pfeile ge-
kennzeichnet. Ausgehend von a=2 erhält man die Elemente der Folge, indem man je mit der
Schrittweite a=2 im Uhrzeigersinn weitergeht. Wesentlich für die Existenz des multiplikativ
inversen Elements ist, dass einer der Pfeile auf das Element 1 zeigt. Anschaulich sehen wir in
Abb. 2-2, dass der Zyklus der Pfeil-Folge nicht in mehrere gleiche Teilzyklen zerfallen kann,
weil die Zahl n=p=5 der Punkte auf dem Kreis als Primzahl nicht teilbar ist. Damit zeigt einer
der Pfeile auf das Element 1.
(5a)
0
(2a)
(3a)
4
1
Abb. 2-2: Folge der Produkte 1·a, 2·a, 3·a, …
für die Wahl a=2 im Zyklus der Elemente
modulo 5 von n=p=5.
Wir sehen in dem Beispiel, dass (3·a) mod 5
auf den Wert 1 fällt. Somit ist a
1
=3 das mul-
tiplikativ inverse Element zu a=2.
3
2
(4a)
(1a)
Verallgemeinernd kann man argumentieren: Die Zahl n der Punkte auf dem Kreis und die
Folge der Pfeile mit der Schrittweite a haben eine gemeinsame Periode, die durch das kleinste
gemeinsame Vielfache kgV von n und a angegeben wird. Es ist kgV = n·a, falls n und a relativ
prim zueinander sind, d.h. falls der größte gemeinsame Teiler ggT von n und a den Wert 1 hat.
kgV(n, a)
n a
für
ggT(n, a)
1,
d.h. für
(n, a) relativ prim
(2.1-9)
Die gemeinsame Periode umfasst n Schritte je mit der Schrittweite a. Die Periode der Pfeile hat
die Länge n. Damit werden alle Punkte im Kreis genau einmal berührt und damit auch das
Einselement. Die Aussage von (2.1-8) können wir jetzt noch erweitern:
1
Für jedes Element a
0 gibt es mod n ein multiplikativ inverses Element a
,
(2.1-10)
falls
ggT(n, a)
1,
d.h. (n, a) relativ prim
Das heißt, auch wenn n keine Primzahl ist, gibt es zu Elementen a multiplikativ inverse Ele-
mente a
1
, falls a und n teilerfremd sind.