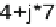Cryptography Reference
In-Depth Information
x
1 2
(b
p
a
q) mod n
n
p q
ggT(p, q)
1
(4.1-24)
x(b
!
a)m dn
1
p
!2
q
Die Faktoren p und q brauchen nicht Primzahlen zu sein. Es genügt, dass sie zu einander teiler-
fremd sind, also keine gemeinsamen Faktoren enthalten.
Beweis
Wir schreiben (4.1-24) um und wenden mod p an.
((x
12
b
p
a
q) mod n) mod p
0
(4.1-25)
In (4.1-25) können wir „mod n“ weglassen, denn wenn die linke Seite durch p teilbar ist,
(...)mod p=0, dann ist sie auch durch ein Vielfaches von p teilbar, also durch n teilbar. Weiter
ersetzen wir entsprechend (4.1-22) Vielfache von p durch 0:
(x
11
b
p
a (1
p)) mod p
(x
0
a (1
0)) mod p
0
(4.1-26)
(x
a) mod p
0
Das Ergebnis (x
a) mod p
0
stimmt mit (4.1-23) überein. (x
b) mod q
0
ergibt sich in
entsprechender Weise.
Ausgehend von a=(x)mod p und b=(x)mod q in (4.1-23) gilt der zu beweisende Satz (4.1-24)
sowohl mod p als auch mod q. Da die Faktoren p und q von n=p·q teilerfremd sind, gilt der zu
beweisende Satz (4.1-24) auch modulo n.
Beispiel für den Chinesischen Restsatz
Es sei gegeben:
p
3, q
7,
damit
n
p q
21
axm d32
bxm d74
Ohne den Chinesischen Restsatz können wir feststellen, dass das Ergebnis x die Angaben für a
und b erfüllen muss, die wir als Bedingungen umschreiben:
xaip2i3
xbiq4i7
In dem folgenden Diagramm sind die beiden Bedingungen durch Pfeile dargestellt. Wir sehen,
dass für x=11 beide Bedingungen erfüllt sind und damit x=11 die Lösung ist.