Cryptography Reference
In-Depth Information
this study clarifies fundamental issues regarding security in a multi-
party environment. Secondly, it draws the lines between what is possible
in principle and what is not. Thirdly, it develops general techniques
for designing secure protocols. And last, sometimes, it may even yield
schemes (or modules) that may be incorporated in practical systems.
REAL MODEL
IDEAL MODEL
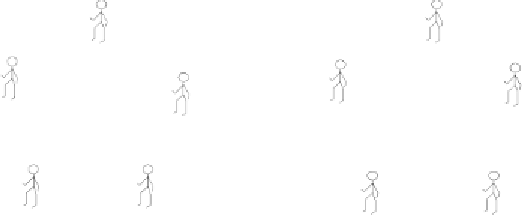
Fig. 7.1 Secure protocols emulate a trusted party - an illustration.
A general framework for casting (
m
-party) cryptographic (protocol)
problems consists of specifying a random process
1
that maps
m
inputs
to
m
outputs. The inputs to the process are to be thought of as the local
inputs of
m
parties, and the
m
outputs are their corresponding (desired)
local outputs. The random process describes the desired functionality.
That is, if the
m
parties were to trust each other (or trust some external
party), then they could each send their local input to the trusted party,
who would compute the outcome of the process and send to each party
the corresponding output. A pivotal question in the area of crypto-
graphic protocols is to what extent can this (imaginary) trusted party
be “emulated” by the mutually distrustful parties themselves.
1
That is, we consider the secure evaluation of randomized functionalities, rather than
“only” the secure evaluation of functions. Specifically, we consider an arbitrary (ran-
domized) process
F
that on input (
x
1
, ..., x
m
), first selects at random (depending only
on
de
=
i
=1
|x
i
|
)an
m
-ary function
f
, and then outputs the
m
-tuple
f
(
x
1
, ..., x
m
)=
(
f
1
(
x
1
, ..., x
m
)
, ..., f
m
(
x
1
, ..., x
m
)). In other words,
F
(
x
1
, ..., x
m
)=
F
(
r, x
1
, ..., x
m
), where
r
is uniformly selected in
{
0
,
1
}
(with
=poly(
)), and
F
is a function mapping (
m
+1)-
long sequences to
m
-long sequences.