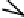Cryptography Reference
In-Depth Information
easy
x
f(x)
HARD
Fig. 2.1 One-way functions - an illustration.
2.1
One-way functions
One-way functions are functions that are eciently computable but
infeasible to invert (in an average-case sense). That is, a function
f
:
{
}
∗
is called
one-way
if there is an ecient algorithm
that on input
x
outputs
f
(
x
), whereas any feasible algorithm that tries
to find a preimage of
f
(
x
) under
f
may succeed only with negligible
probability (where the probability is taken uniformly over the choices
of
x
and the algorithm's coin tosses). Associating feasible computations
with probabilistic polynomial-time algorithms, we obtain the following
definition.
}
∗
→{
0
,
1
0
,
1
}
∗
→{
}
∗
Definition 2.1.
(one-way functions):
A function
f
:
{
0
,
1
0
,
1
is called
one-way
if the following two conditions hold:
(1)
easy to evaluate:
There exist a polynomial-time algorithm
A
such that
A
(
x
)=
f
(
x
)forevery
x
}
∗
.
(2)
hard to invert:
For every probabilistic polynomial-time algo-
rithm
A
,everypolynomial
p
, and all su
ciently large
n
,
∈{
0
,
1
1
p
(
n
)
Pr[
A
(
f
(
x
)
,
1
n
)
f
−
1
(
f
(
x
))]
<
∈