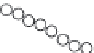Information Technology Reference
In-Depth Information
10
0
10
0
10
-2
10
-2
α
=
3/2
α
=
3/2
10
-4
10
-4
10
-6
Darwin
Einstein
10
-6
10
-8
10
0
10
1
10
2
10
3
10
4
10
0
10
1
10
2
10
3
Response time
10
4
10
5
Response time
τ
(days)
τ
(days)
Figure 6.3.
The graphs indicate the distributions of response times to letters by Darwin (left) and Einstein
(right). These distributions have the same meaning as the waiting-time distribution density
introduced earlier. This figure was adapted from [
27
] with permission.
holds only for a limited time regime, whereafter it is followed by an exponential decay.
More remarkable is the fact that Oliveira and Barabási [
27
] found that the time interval
between the receipt of a letter by either Darwin or Einstein and the sending of their
replying letters is satisfactorily described by waiting-time distribution densities with
μ
=
5, as depicted in Figure
6.3
. Both Darwin and Einstein began writing letters as
teenagers and the volume of letters sent and received tended to increase as a function of
time.
Barabási numerically studied the limiting case of
p
1
.
1, namely the case in which at
any time step the highest-priority customer is served, and determined in this case that
the waiting-time distribution is the inverse power law
=
1
τ
.
ψ(τ)
∝
(6.24)
Note that
p
1 is a singularity that on the one hand makes the exponential cutoff
diverge and on the other hand generates a
=
of vanishing amplitude. Thus, Vásquez
[
33
] and Gabrielli and Caldarelli [
17
] developed special methods to derive the power-
law index
ψ(τ)
1 without these limitations.
On the basis of the fact that on moving from the totally random to the totally determin-
istic condition the waiting-time distribution changes its structure from the exponential
form (
6.19
) to the inverse power law with index
μ
=
1 (that Barabási found to be
a proper description of the email communication [
8
]), Barabási decided to refine his
model so as to study the cases intermediate between random choice of the task and the
highest-priority-task criterion. He adopted for the probability that a task with priority
x
is chosen for execution per unit time the prescription
μ
=
x
γ
N
(
x
)
=
.
(6.25)
i
=
1
x
i
Note that in this section we are identifying Barabási's tasks with the
N
lines moving
in lanes of equal width
L
in a post office, in the normalized interval [0, 1]; see Figure
6.4
.