Information Technology Reference
In-Depth Information
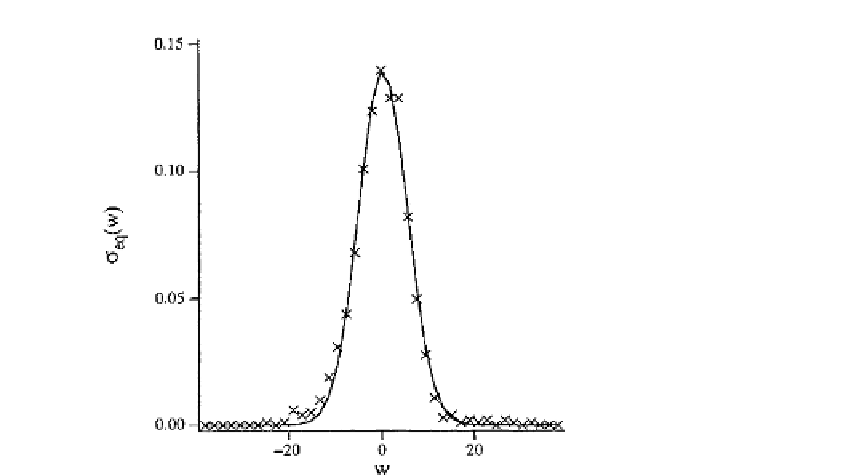
Figure 4.19.
The equilibrium distribution function of the velocity variable
w
for network-bath coupling
strength
γ
= 0.01. The crosses denote the results of the computer calculations of the mapping
(
4.104
). The full line is a Gaussian function with the width 38.5, which has to be compared with
the theoretical prediction 32.0 [
7
]. Reproduced with permission.
the Gaussian function of Figure
4.19
. The width of this “experimental” function turns
out to be
2
2
(
w
eq
)
fit
=
38
.
5, compared with the theoretical value
w
eq
=
32 obtained
later.
Thus, on the basis of our numerical calculations, and within the specific limits set
by them on the determination of the higher-order moments, we can consider the system
(
4.104
) to be equivalent to the Langevin equation (
3.52
).
One of the purposes of this topic is to establish the theoretical reasons for the equiv-
alence found between the two ways of determining the width of the Gauss distribution
for a fluctuation-dissipation process. Another way to say this is that we know from
the fluctuation-dissipation relation that the width of the Gauss distribution is propor-
tional to the temperature of the environment for a Brownian particle. So why should the
strength of the fluctuations produced by the booster give rise to a physical temperature?
We address this question later.
The prototype booster
Let us again consider the network described by the equations of motion (
4.100
), that is,
the network with the Hamiltonian (
4.105
), which we rewrite here:
1
2
m
1
π
1
2
m
2
v
2
2
H
=
+
+
U
(ξ,ζ,).
(4.112)
The behavior of this network at a fixed value of the mechanical energy
E
is investi-
gated in the domain where the parameter values give rise to chaotic dynamics. Since the
energy
E
is a constant of the motion, the four variables
ξ,ζ,π
and
v
are not independent