Information Technology Reference
In-Depth Information
0.75
0.50
0.25
0.00
-1.0
-0.5
0.0
0.5
1.0
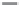
Figure 3.4.
A double-well potential is depicted for three different values of the parameter controlling the
barrier height between the wells. The parameters have been adjusted so that the well minima are
at
±
0
.
50 and the maximum is at zero.
barrier done by Kramers in the case of the double-well potential. Kramers applies the
Smoluchosky approximation and adopts the Langevin equation given by (
3.95
), where
U
is the potential sketched in Figure
3.4
.
The rate at which a population of chemicals makes a transition from one well to the
other due to thermal excitations is estimated here using Kramers' theory. We note that
this is not an exact analytic calculation and that it includes an approximation of the
shape of the double-well potential. However, numerical calculations of the rate of tran-
sition and of its dependence on the strength of the thermal fluctuations and the height of
the barrier between the two wells compare very well with Kramers' rate. The Kramers
theory is too specialized to explore here in detail, but the double-well potential has
found numerous useful modeling applications. One such application involved climate
change, for which a new physical concept was introduced by Benzi and Vulpiani [
7
].
They were trying to understand whether a relatively small periodic force can be ampli-
fied by internal nonlinear interactions in the presence of noise. The mechanism they
identified as stochastic resonance (SR) applied to the understanding of the Milankovitch
cycle, whose period of 10
5
years is observed in climate records. This mechanism was
independently identified and applied to the same problem by Nicolis and Nicolis [
37
].
However, the potential importance of the SR mechanism did not become apparent until
after the article by Moss and Wiesenfeld [
35
] on the neurologic applications of SR.
It is possible to begin the analysis of SR from a Hamiltonian having a double-well
potential and a periodic forcing term to change (
3.95
)into
dQ
dt
=−
(
Q
)
A
λ
(
A
p
λ
Q
2
a
2
−
)
Q
+
cos
(ω
p
t
)
+
η(
t
)
(3.96)
and here too we have included the coupling to the environment. Note that (
3.96
)
describes a particle in a time-dependent potential
A
4
Q
A
p
λ
Q
2
a
2
2
(
Q
)
=
λ
(
−
)
−
cos
(ω
p
t
).
(3.97)
We leave the description of how the potential behaves as Problem 3.3. From (
3.96
)
we see that the particle oscillates in the vicinity of one of the minima and the poten-
tial rhythmically changes the relative position of the minima. If the change in minima
matches the fluctuations, a particle can be propelled over the potential barrier. This