Algorithmics - The Computing Universe: A Journey through a Revolution - page 99

we do not have to try all the choices to find the right solution. As we can see
from the fact that it is easy to check whether or not we have a correct solution,
this nondeterministic method can find the solution in polynomial time. This is
why these problems are called NP - since there is a nondeterministic polyno-
mial solution.
The second property of NP-complete problems is perhaps the most remark-
able. No one has been able to prove that there does not exist a polynomial time
algorithm for any of these problems. What the designation complete signifies is
that if a polynomial time solution were found for one of these problems, then
there would be a polynomial time algorithm for all of them! How does this
come about? Let us look at another path-finding problem, one that does not
involve distances. If we are given a graph consisting of points and edges, can
we find a path that passes through all the points exactly once? Such a path is
called a Hamiltonian path , after the great Irish mathematician William Hamilton.
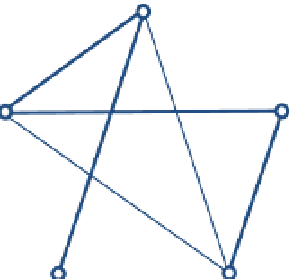
Figure 5.18a shows a Hamiltonian path through five nodes. This problem also
turns out to be intractable and NP-complete. Curiously, if we want a path that
goes through all the edges exactly once - called an Eulerian path , as in Euler's
solution to the Bridges of Königsberg problem - the situation is very different.
Euler found a polynomial time algorithm for this problem in 1736!
As we have said, the complete in NP-complete signifies that all the prob-
lems stand or fall together. Either all NP-complete problems are tractable or
none of them are. The concept that is used to establish this is to show that
there is a polynomial time algorithm that reduces one NP-complete problem
to another. We can see how this works by reducing the Hamiltonian path
problem to the traveling salesman problem. In Figure 5.18a we have a graph
with five nodes and we have highlighted the Hamiltonian path for this graph.
We can construct a traveling salesman network from this graph by using the
same nodes, but also drawing additional edges connecting every two nodes
as in Figure 5.18b . We assign cost 1 to an edge if it was originally present and
cost 2 for each new edge we have added. The new graph has a traveling sales-
man shortest path of length 6 units - in general N + 1 where N is the number
of nodes in the graph - if the original graph had a Hamiltonian path. Thus
the answer to whether or not there is a tour no longer than N + 1 is the same
as asking whether or not the graph contains a Hamiltonian path. Since the

B.5.7. Steven Cook received the
Turing Award in 1982 for his con-
tribution to algorithmic complex-
ity research.

1 2

1

1

1

1 2

Fig. 5.18. (a) The Hamiltonian path
(in bold) connecting five nodes goes
through each node exactly once. (b) The
Hamiltonian path problem can be con-
verted into a TSP by adding extra edges
as described in the text. The traveling
salesman tour is shown in bold. (Figure
courtesy of David Harel.)

1

2

2

(a)

(b)