Algorithmics - The Computing Universe: A Journey through a Revolution - page 92

for the start and finish landmasses, the number of bridges connecting any
other landmass must be an even number - half of the bridges for the walker
to enter the landmass, and half for the walker to leave it. In the case of the
bridges in Königsberg, we see that all the four landmasses are connected by
an odd number of bridges - one by five, the other three by three. Because at
most two of the landmasses can be the starting and end points, we see imme-
diately that it is not possible to walk through the city crossing each bridge
exactly once.
Let us look at another important type of graph problem. This is the prob-
lem of finding the minimal spanning tree (MST) - a path that reaches every
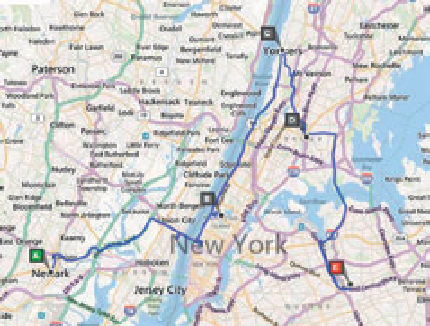
node in a graph with the minimum cost. Consider five well-known communi-
ties in the area around New York City ( Fig. 5.8a ) and represent them as a graph
( Fig. 5.8b ). In this graph, each community is represented as a vertex, with a
road joining two communities by an edge. Each edge is assigned a number rep-
resenting the “cost” needed to go between the communities at the ends of each
edge. This could represent the cost of a cable connection or the time of travel
between the two places, for example.
Imagine that the company wants to connect its offices in the five com-
munities using the least amount of optical fiber. The minimal spanning tree
(MST) solves this problem. Finding the MST is a problem that can be solved by
using a so-called greedy algorithm. Greedy algorithms take the optimal choice
at each local stage of the algorithm and in general are not guaranteed to find
the globally best solution but can be proved to do so for the case of the MST. In
this example, we start with the shortest edge in the graph; then from the two
vertices at the ends of this edge, we choose the next shortest edge. We continue
to add to the resulting graph by adding the next shortest edge that has not yet
been considered. We repeat this procedure until we have visited each city in
the graph. The result is the MST shown in Figure 5.9 .
The solution illustrates another important structure in computer science:
trees. Trees are similar to graphs except that they do not contain closed loops.
Trees are found everywhere in our daily lives, such as in the organization charts
of companies or in the file structures on your computer ( Fig. 5.10 ). Efficient
algorithms to traverse and manipulate tree structures are an important area of
algorithmics ( Fig. 5.11 ).

Fig. 5.8. An illustration of the MST prob-
lem. The figure shows (a) five communi-
ties in the New York area: A = Newark;
B = Manhattan; C = Yonkers; D = The
Bronx; E = Queens; and (b) a graph of
the five communities with distances allo-
cated to each edge.

(a) (b)

A

100

10

30

B

E

50 10 60

C D

20