Graphics Reference
In-Depth Information
9.3.2
Rotation with Arbitrary Pivot
We can apply the lessons we have learned in scaling directly to rotation. Recall
that when operating on an input vertex
V
a
, the rotate operator
R
(
θ
)
would:
R
i
pr
(
θ
)=
x
a
cos
θ
.
R
o
V
a
R
θ
−
y
a
sin
θ
y
a
cos
θ
+
x
a
sin
T(-8,-3)
Now, if
V
a
is the origin, where
V
a
=
x
a
y
a
=
00
,
T(8,3
)
R
t
R
tr
R(45
o
)
then
(
θ
)=
0
θ
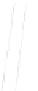
Figure 9.8.
Rotation
with pivot at the top right
of
R
i
.
R
t
is the translated
R
i
,
R
tr
is the rotated rectan-
gle from
R
t
,and
R
o
is the
rotation result.
V
a
R
×
cos
θ
−
0
×
sin
θ
0
×
cos
θ
+
0
×
sin
=
00
=
.
This observation says that the origin position will not be changed by a rotation
operator. In another words, by default, the origin is the center of rotation, or the
pivot position. Based on what we have learned from scaling, we know that we
can apply translation before and after the rotate operator to strategically select the
pivot position. Now we can define the pivoted rotation operator
R
pt
(
θ
)
V
a
,where
R
i
pc
R
pt
(
θ
)=
T
(
−
pt
.
x
,−
pt
.
y
)
R
(
θ
)
T
(
pt
.
x
,
pt
.
y
)
.
(9.5)
R
o
T(-2,-6.5)
Once again,
=
pt
y
T(2,6.5)
pt
.
xpt
.
R
t
R
tr
is the pivot position. With the pivoted rotation operator, we can now rotate any
collection of vertices centered at any chosen pivot position. For example, Fig-
R(45
o
)
ure 9.8 shows the results of applying
Figure 9.9.
Rotation
with pivot at the center of
R
i
. As in Figure 9.8,
R
t
is
the translated rectangle
R
i
,
R
tr
is the rotated rectangle,
and
R
o
is the result.
45
◦
)
,
R
pr
(
where
=
38
,
pr
or rotating
R
i
with the top-right corner being the pivot position. As we saw in
pivoted scaling, by translating the pivot vertex to the origin before we apply the
rotation, we can accomplish the desired and more intuitive rotation. Figure 9.9
shows another example of
R
pc
(
45
◦
)
, with
=
26
5
,
pc
.
the center of the rectangle
R
i
.



































































































































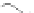






















Search WWH ::

Custom Search