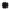Graphics Reference
In-Depth Information
Figure 2.12.
A glide reflection.
B¢
L
A¢
B
A
sends the origin to
p.
Let M¢ = T
-1
M. Then M¢ is an orientation-reversing motion that
fixes the origin and hence a reflection by Lemma 2.2.7.3. Since M = TM¢, M is a glide
reflection and we are done.
2.2.7.5. Theorem.
Every motion M is either a translation, rotation, reflection, or
glide reflection.
Proof.
If M is a rigid motion, then M is a translation or rotation by Theorem 2.2.6.2.
If M is not a rigid motion, that is, if it is orientation reversing, then M is a reflection
or glide reflection by Theorem 2.2.7.4.
One final word about why the term “congruent transformation” is sometimes used
instead of “motion.” The reader may recall the notion of “congruent figures” from
his/her Euclidean geometry course in high school, which most likely was never given
a really precise definition. Well, we can do so now.
Definition.
Two figures are said to be
congruent
if there is a motion that carries one
into the other.
2.2.8
Frames in the Plane
Before leaving the subject of motions in the plane we want to discuss another
approach to defining them - one that will be especially powerful in higher dimen-
sions.
Definition.
A
frame
in
R
2
is a tuple F = (
u
1
,
u
2
,
p
), where
p
is a point and
u
1
and
u
2
define an orthonormal basis of
R
2
. If the ordered basis (
u
1
,
u
2
) induces the standard
orientation, then we shall call the frame an
oriented frame
. The lines determined by
p
and the direction vectors
u
1
and
u
2
are called the
x-
, respectively,
y-axis
of the frame
F. The point
p
is called the
origin
of the frame F. (
e
1
,
e
2
,
0
) is called the
standard frame
of
R
2.
To simplify the notation, we sometimes use (
u
1
,
u
2
) to denote the frame (
u
1
,
u
2
,
0
).
Frames can be thought of as defining a new coordinate system. See Figure 2.13.
They can also be associated to a transformation in a natural way. If F = (
u
1
,
u
2
,
p
) is a
frame and if
u
i
= (u
i1
,u
i2
) and
p
= (m,n), then define a map T
F
by the equations
x uxuym
¢=
+
+
11
21
y uxuyn
¢=
+
+
.
(2.20)
12
22