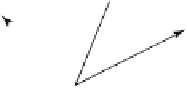Graphics Reference
In-Depth Information
(
)
=
()
+
(
,
Ma
uv
+
b
aM
u
bM
v
for all vectors
u
and
v
and real numbers a and b.
Proof.
We shall show that M is a linear transformation in two steps.
Claim 1.
M(
u
+
v
) = M(
u
) + M(
v
).
Define a vector
w
by the equation
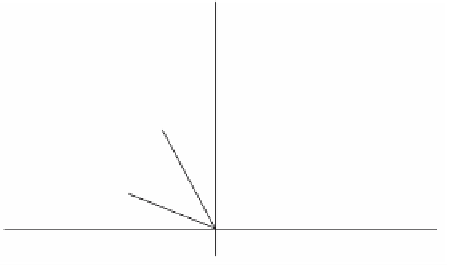
uv w
+=2.
(2.15)
This equation can be rewritten as
1
2
(
)
wu
=+
vu
-
.
(2.16)
See Figure 2.6. Since M(
0
) =
0
(which implies that |M(
p
)| = |
p
| for any vector
p
), we
can use equation (2.15) and Lemma 2.2.2 to conclude that
(
)
=
()
M
uv
+
2
M
w
.
(2.17)
Similarly, equation (2.16) and Lemma 2.2.2 implies that
1
2
()
=
()
+
(
()
-
()
)
MM
wu
MM
v
u
.
(2.18)
Substituting the expression for M(
w
) in equation (2.18) into equation (2.17) and sim-
plifying the result proves Claim 1.
Claim 2.
M(c
v
) = cM(
v
), for any real number c.
This follows from Lemma 2.2.2 (let
A
=
0
,
B
=
v
, and t = c in that Lemma). Theorem
2.2.4.1 is proved.
u + v
M(u + v) = 2M(w)
M(v)
u
w
M (w)
v
M(u)
Figure 2.6.
Proving motions are linear
transformations.