Graphics Reference
In-Depth Information
Let f Œ
C
[X
1
,X
2
,...,X
n
] and
V
= V(f) Õ
C
n
.
10.3.6. Theorem.
(1) The (projective) hypersurface V(H(f)) in
P
n
(
C
) is the projective completion
H(
V
) of
V
.
(2) The projective completion H(
V
) of
V
is the topological closure of
V
in
P
n
(
C
).
(3) Using the notation defined by equations (10.23), j
-
n+1
(
V
) = D(H(
V
)). (Basically,
this says that
V
is the affine part of the projective completion of
V
.)
Proof.
See [Kend77] or [Shaf94].
The next example shows that Theorem 10.3.6 is
false
if the field is the reals. The
algebraic closure property of the complex numbers is essential.
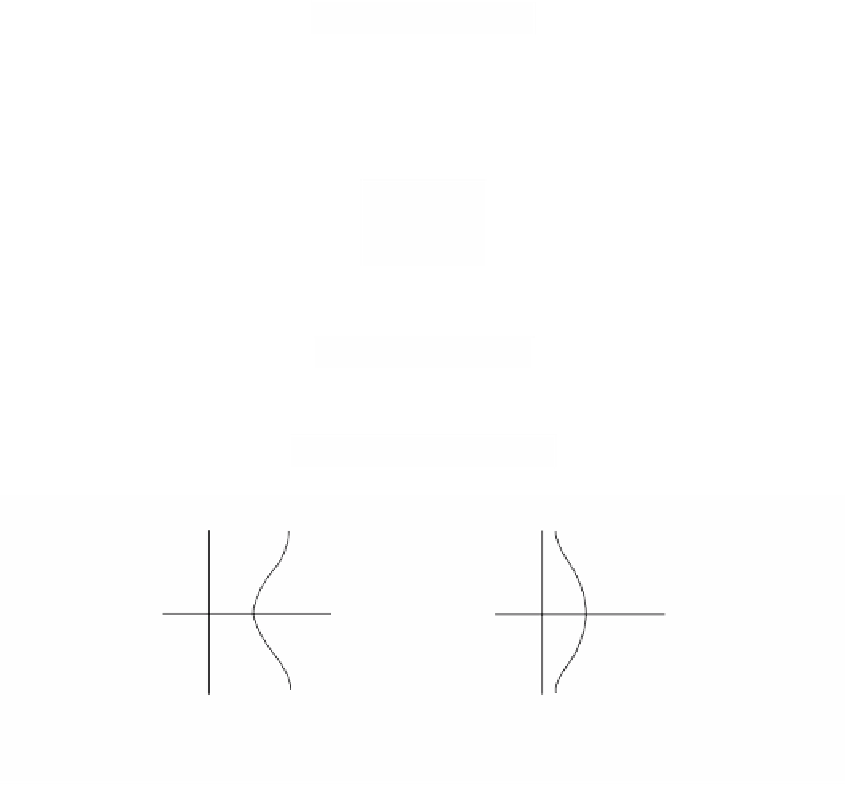
10.3.7. Example.
Consider
(
)
=-
2
2
(
)
fXY
,
Y
X X
-
1
and let
V
= V(f) Õ
R
2
. Figure 10.7(a) shows
V
. Note that the origin is an isolated
point of the graph. It is basically such an isolated point that will lead to our coun-
terexample but it will not be
V
directly because we need a variety that has its isolated
point at infinity. To get this variety we simply move
V
. Consider the transformation
TX Z
YY
ZX
:
¢=
¢=
¢=
,
which moves the y-axis to the line at infinity. This will transform
()
=
2
3
2
Hf
Y Z
-
X
+
X Z
into
(
)
=
2
3
2
GXYZ
,,
Y X Z
-
+
Z X
Y
Y
V = V(f )
W = V(g)
X
X
f(X,Y) = Y
2
- X
2
(X - 1)
g(X,Y) = Y
2
X + X - 1
(a)
(b)
Figure 10.7.
The varieties of Example 10.3.7.