Algebraic Geometry - Computer Graphics and Geometric Modeling - page 683

p • -1 0 +1 p • -1 0 +1

(a) (b)

Figure 10.5. Example 10.2.4.

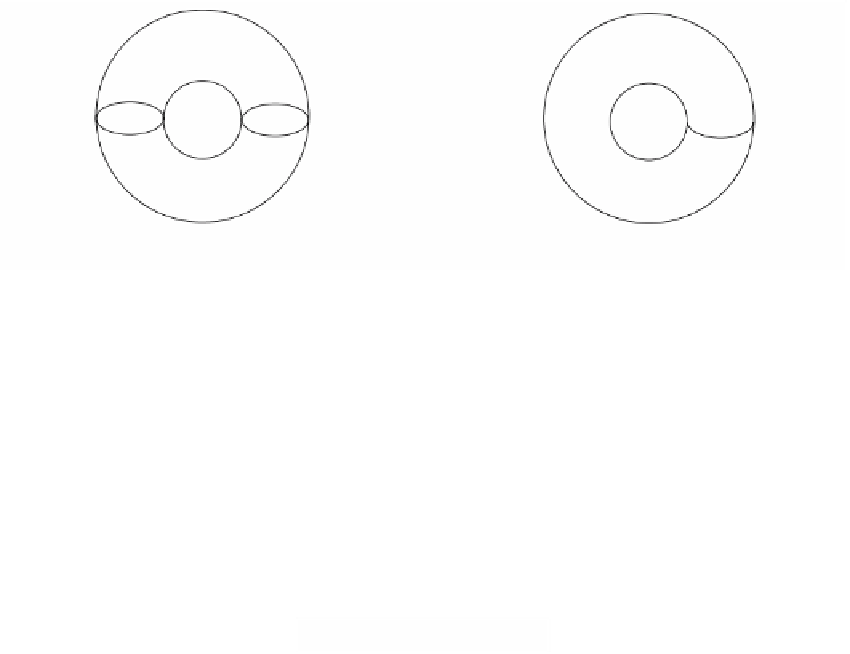
in which possibly a finite number of pairs of points have been identified. In general,
the closure of V(f) is a finite union of such spaces where each is attached to every
other along a finite set of points.

Proof. See [Kend77].

Theorem 10.2.5 tells us what an arbitrary algebraic curve in P 2 ( C ) looks like topo-
logically, but it does not say that every surface of the type described in the theorem
is an algebraic curve, only some are. However, one can use the polynomial

( ) ( )

2 2 2 2

YXX - - 1 ... Xg -

to generate a space of genus g with 2-to-1 identifications. Constructing spaces with
more complicated identifications gets more complicated.
We have just seen that if we want to understand plane curves there is more
than what meets the eye at first glance. A similar revelation can be had with respect
to the problem of plane curve intersections. Two distinct lines (degree 1 curves)
can intersect in a single point or none at all. A line and a conic can intersect in 2, 1,
or 0 points. Figure 10.6 shows some possible intersections of two distinct conics
(degree 2 curves). One can have anywhere from 0 to 4 points in the intersection.
At first glance it would appear that there is no connection between the degree of
the curves and the number of points in their intersection. However, there is a
connection. The problem again is that the reals are not algebraically closed. If we
think of the curves as lying in P 2 ( C ), Bézout's theorem (Theorem 10.7.4) will tell us
that there are as many points in the intersection, if counted with their multiplicities,
as the product of the degrees of the curves. For example, in P 2 all distinct lines
intersect in a point. Also, in P 2 , the line that corresponds to the y-axis in R 2 and
the conic that corresponds to the parabola y = x intersect at the origin and the ideal
point [0,1,0].
These preliminary observations should be an indication of the rich theory await-
ing us and we now proceed to a more rigorous analysis. Hopefully, the examples in
this section have justified our earlier comments about the need to understand things
at the complex number and projective space level. Life is easier there and there is