Graphics Reference
In-Depth Information
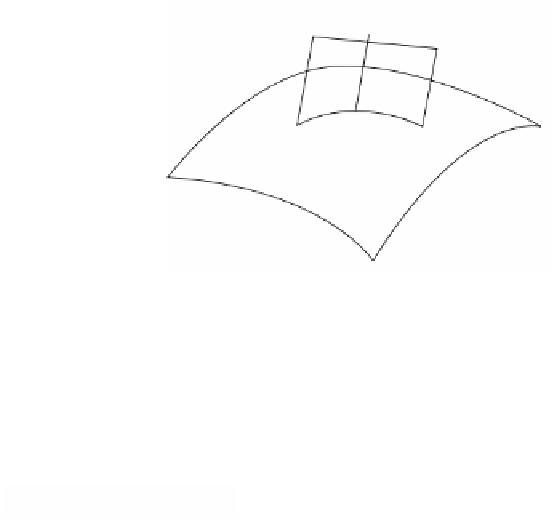
Figure 9.18.
Normal curvatures at a point.
n
p
X
u
p
u
S
Euler's Theorem.
As
u
ranges over all unit vectors in the tangent plane to
S
at
p
,
the set of curvatures k
u
, called
normal curvatures
, forms a closed interval [k
1
,k
2
]. If
the k
u
are not all equal, then there is precisely one direction
u
1
for which the associ-
ated curve has the minimum curvature k
1
and one direction
u
2
for which the associ-
ated curve has the maximum curvature k
2
. Furthermore,
u
1
and
u
2
are orthogonal
and if a unit vector
u
makes an angle q with
u
1
, then
2
2
kk k
u
=
cos
q
+
sin
q
.
(9.41)
1
2
Definition.
The curvatures k
1
and k
2
are called the
principal normal curvatures
of
S
at
p
. and the radii of the associated osculating circles are the
principal radii
. The
vectors
u
1
and
u
2
are called the
principal normal directions
of
S
at
p
.
Note that if we change the direction of the normal
n
p
, then the sign of the cur-
vatures k
u
changes, but all the results remain valid. Another interesting fact is that
we really did not have to consider planar curves (curves that lie in
X
u
), but any para-
metric curve in
S
through
p
that has tangent vector equal to
u
would give rise to the
same curvature k
u
.
Let
c
u
denote the center of curvature at the point
p
of the planar curve that was
used to define the normal curvature k
u
. The centers
c
u
lie on the line normal to
S
at
p
, so that
c
u
=
p
+ t
u
n
p
for some t
u
Œ
R
. The set of these centers as
u
ranges over all
unit vectors in the tangent plane consists of one or two closed intervals. More pre-
cisely, there exist numbers
t
and
t
,
-•£
t
£
t
£•
,
min
max
min
max
so that the set of centers is either
[
]
[
]
»•
[
]
cc
,
or
-•
,
c
c
,
,
min
max
min
max
where
c
min
=
p
+ t
min
n
p
and
c
max
=
p
+ t
max
n
p
. The points
c
min
and
c
max
are the centers
of circles that define the principal normal curvatures k
1
and k
2
, respectively. See Figure
9.19. The point
p
in Figure 9.19(a) is called an
elliptic point
of the surface because the
surface lies to one side of the tangent plane and meets the tangent plane in a single
point locally. The point
p
in Figure 9.19(b) is called a
hyperbolic point
because the