Graphics Reference
In-Depth Information
9.5
Envelopes of Curves
Envelopes of families of curves or surfaces were an important part of classical dif-
ferential geometry, especially in the development of the concept of a connection which
is fundamental to modern differential geometry. See [Spiv75]. They also appear in the
context of cyclides and developable surfaces. Even so, they have only been studied to
a limited degree, mainly envelopes of circles, planes, and spheres. An analysis can get
very tricky even in very simple sounding situations. We consider envelopes here
because of their relevance to CAGD.
This section looks at envelopes of planar curves. Section 9.11 considers envelopes
of surfaces.
Definition.
Let a
t
: [0,1] Æ
R
2
be a one-parameter family of curves in the plane
defined by a
t
(u) =a(u,t) for some C
•
function a : [0,1] ¥ [0,1] Æ
R
2
. An
envelope
of this
family is defined to be a curve p(u) that is not a member of this family but that is
tangent to some member of the family at every point.
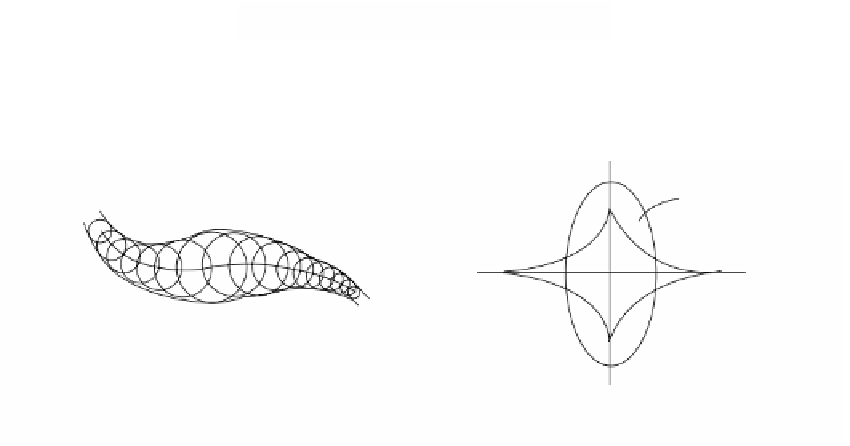
See Figure 9.8(a). Unfortunately, the envelope can have bad singularities like cusps
even if a is a nice function. See Figure 9.8(b), which shows the envelope of normals
to an ellipse whose ends are the centers of the osculating circles.
The classical approach to studying the envelope p(u) is geometric. Basically,
one defines p(u) to be the limit as e approaches 0 of the intersections of a
t
(u) and
a
t
(u +e). Such a definition can have serious problems in general, but seems to work
in many cases of interest.
Let us start off with a special case that will not only make the argument clearer
but will also be used for the general case since that case will reduce to this one. Assume
that the curves a
t
are graphs of functions f
t
, that is,
()
=
(
)
=
()
=
()
a u t
,
u v
,
,
where v
f u t
,
f u
.
t
If the curve a
t
intersects the curve a
t+h
at the point (u
h
,f(u
h
,t)) = (u
h
,f(u
h
,t + h)),
then
envelope
of normals
of ellipse
(a)
(b)
Figure 9.8.
Envelopes.