Graphics Reference
In-Depth Information
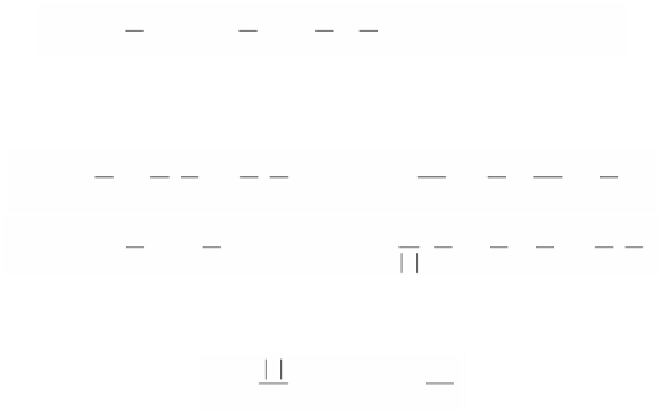
Second, B • T = 0 implies that
BT BT
¢∑
=-
∑ ¢=-
B N
∑
k
=
0.
Therefore, B¢ is orthogonal to both B and N. Since (T,N,B) is an orthonormal basis,
it follows that B¢ must be some multiple of N.
Definition.
The function t(s) in Proposition 9.4.2 is called the
torsion
of F
at s.
The minus sign in Proposition 9.4.2 is there so that (T(s),N(s),F¢≤(s)) determines
the standard orientation whenever t(s) > 0. See equation 9.16 below.
The curve in
R
3
parameterized by
9.4.3. Example.
F
()
=
(
)
a cos t,a sin t,bt ,
where a and b are nonzero constants is called a
helix
. Let us compute the curvature
and torsion of this helix.
Solution.
First, we find the arc-length parameterization G(s) of the helix using the
method described in Section 9.2. We get
s
D
s
D
s
D
b
s
D
Ê
Ë
ˆ
¯
=
Ê
Ë
ˆ
¯
()
=
2
2
Gs
F
a cos
,
a sin
,
,
where
D
=+
a
b
.
It follows that
a
D
s
D
a
D
s
D
b
D
a
D
s
D
a
D
s
D
Ê
Ë
ˆ
¯
Ê
Ë
ˆ
¯
()
=-
¢
()
=-
Ts
sin
,
cos
,
,
Ts
cos
,
-
sin
,
0
,
2
2
s
D
s
D
a
a
b
D
s
D
b
D
s
D
a
D
Ê
Ë
ˆ
¯
Ê
Ë
ˆ
¯
()
=-
()
=
Ns
cos
,
-
sin
,
0
,
and
B s
sin
,
-
cos
,
.
It is now easy to show that
a
D
b
D
()
=
()
=
k
s
and
t
s
2
.
2
and we are done.
Since B is orthogonal to the osculating plane, and |t(s)| = |B¢(s)|, we can think of
t(s) as measuring the rate at which the osculating plane is changing. In other words,
t(s) measures by how much the curve deviates from being planar.