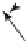Graphics Reference
In-Depth Information
y
N
i
a
i
N
i-1
p
i
N
i
N
i-1
a
i
S
1
p
i+1
L
i
x
p
i-1
midpoints
(a)
(b)
Figure 9.6.
The curvature at vertices of polygonal curves.
()
= 2p deg
k
T
L
T
.
Proof.
See [Stok69], [Spiv70b], or [Gray98].
Theorem 9.3.13 can be thought of as a kind of integrality theorem because it states
that k
T
/2p is an integer.
9.3.14. Corollary.
For a simple closed curve k
T
= 2p.
Closely related to the total curvature is the concept of the winding number of a
curve F(t) about a point
p
. This measures the angle that the vector F(t) -
p
sweeps
out around the origin. See [AgoM76].
This section described several ways to define the curvature of smooth planar
curves. In closing, we would like to indicate how one could define curvature for poly-
gonal curves. In some sense, one can think of the polygonal concept as a precursor
of the smooth one. Consider a polygonal curve defined by a sequence of points
p
0
,
p
1
,
...,
p
n
. Figure 9.6(a) shows an example. Any curvature for such a curve would be con-
centrated at the vertices and zero elsewhere. At a vertex
p
i
it is natural to use the
signed angle
=-
(
)
a
i
pppp
1
,
s
i
-
i
i
i
+
1
between the directed segments as a measure of how much the curve is turning. But
the lengths of the segments also play a role, so we need to normalize things. Define
the
curvature
K
i
at
p
i
by
a
1
2
i
i
(
)
K
=
,
where
L
=
pp pp
+
.
i
i
i
-
1
i
i
i
+
1
L
If
N
i
is the “outward” unit normal to the segment [
p
i-1
,
p
i
], then a
i
is the length of the
arc from
N
i-1
to
N
i
in the unit circle
S
1
. See Figure 9.6(b). This curvature has some
interesting properties and is the one-dimensional analog of the Gauss curvature for
surfaces defined in Section 9.9. The reader should look back at these comments when