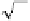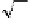Graphics Reference
In-Depth Information
Equation (9.3) states an especially handy relationship because it allows us to replace
differentiation with respect to arc-length by a differentiation with respect to the actual
parameter at hand.
9.2.8. Example.
To find the arc-length parameterization of the function
pp
È
Í
˘
˙
()
=
(
)
F t
sin t,sin t ,
t
Œ-
4
,
4
,
[
(
) (
)
]
which parameterizes the segment
-
12121212
,
-
,
,
.
Solution.
We have
t
Ú
¢
()
s
=
F t dt
-
p
4
t
Ú
=
2 cos t dt
-
p
4
t
=
2 sin t
p
-
4
=
2 sin t
+
1.
It follows that
s1
2
-
-
1
t
=
sin
.
Therefore,
s1
2
-
s1
2
-
1
2
Ê
Ë
Ê
Ë
ˆ
¯
Ê
Ë
ˆ
¯
ˆ
¯
()
=
-
1
-
1
(
)
G s
sin sin
, sin sin
=
s1,s1.
-
-
It is easy to check that this G is an arc-length parameterization.
Example 9.2.8 and the discussion before it show that one can find arc-length
parameterizations in a systematic way, although this may have more of a theoretical
value than a practical one. First, the square root in the integrand in the integral for
arc-length makes that integration difficult in all but the most trivial examples. Second,
finding the inverse of a function is rarely easy. Of course, numeric solutions are
another matter and quite feasible.
9.3
The Geometry of Plane Curves
A natural place at which to start if one wants to understand the geometry of curves
is to try to capture the concept of “curvedness.” We begin with planar curves. So what
exactly should we mean by the curvature of our curve at some point? Just as, for
example, in the case of length where one started by agreeing on what one meant by