Graphics Reference
In-Depth Information
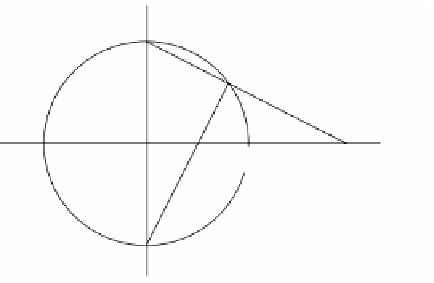
Figure 8.38.
The stereographic
projections of Exercise 8.8.1.
R
n+1
e
n+1
S
n
j
+
-1
(y)
R
n
y
j_ (j
+
-1
(y))
-
e
n+1
See Figure 8.38. Use this to prove that these coordinate neighborhoods induce a
C
•
structures on
S
n
.
Show that the C
•
structures on
S
1
defined in (a) and (b) are the same.
(c)
8.8.2.
Prove the tangent vectors
e
i,
U
defined in the equivalence class of vectors approach to
tangent vectors are a basis for T
p
(
M
).
8.8.3.
Prove that the tangent vectors
∂
/
∂
u
i
defined in equation (8.16) form a basis of the
tangent space.
Section 8.9
8.9.1.
Prove that a trivial n-plane bundles has n linearly independent cross-sections.
8.9.2.
Show that the line bundle g defined in Example 8.9.2 is isomorphic to the open Moebius
strip line bundle described at the beginning of that example.
8.9.3.
Prove the existence of the
continuous
map a in equation (8.27).
8.9.4.
Show that a line bundle is orientable if and only if it is trivial.
8.9.5.
Show that the orientation of a trivial vector bundle over a path-connected space is
uniquely determined once it is specified at one point.
8.9.6.
Let
B
be a contractible space. Show that every vector bundle over
B
is orientable and
that the orientation is uniquely determined once it is specified at one point.
8.9.7.
Let x=(
E
,p,
B
) be an n-plane bundle. Show that both x¥xand x≈xare orientable
vector bundles.
Hint:
Show that if
v
1
,
v
2
,...,
v
n
and
w
1
,
w
2
,...,
w
n
are bases for the fiber p
-1
(
b
) over
some point
b
Œ
B
, then both
v
1
,
v
2
,...,
v
n
,
v
1
,
v
2
,...,
v
n
and
w
1
,
w
2
,...,
w
n
,
w
1
,
w
2
,
...,
w
n
determine the same orientation of p
-1
(
b
) ¥p
-1
(
b
).
Section 8.10
8.10.1. (a)
Show that the alternate description of the tangent bundle of a manifold defined by
equations (8.28) and (8.29) produces a vector bundle that is isomorphic to the orig-
inal definition.
(b)
Show the same thing for equation (8.30).