Graphics Reference
In-Depth Information
Figure 8.33.
Identifying the tangent bundle of
M
with its normal bundle in
M
¥
M
.
p ¥ M
d(M)
M ¥ M
(v
p
,v
p
)
(p,p)
M ¥ p
(v
p
,-v
p
)
closed collar
of ∂M
closed
tubular neighborhood
of M
M
M
∂M
(a)
(b)
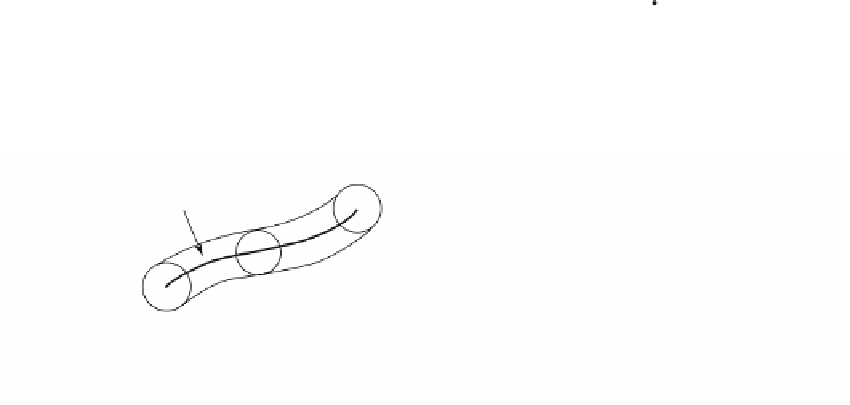
Figure 8.34.
Tubular neighborhoods and collars.
induces a canonical isomorphism from t
M
to n
M
.
Definition.
Let
M
n
be a submanifold of a manifold
N
k
. Suppose that there is a vector
bundle x=(
E
,p,
M
) and an imbedding f :
E
Æ
N
so that f s :
M
Æ
N
is the identity map
on
M
, where s is the zero section of x. If f(
E
) is an open neighborhood of
M
in
N
,
then the pair (x,f) is called a
tubular neighborhood
of
M
in
N
. The associated disk
bundle for x and the restriction of f to that is called a
closed tubular neighborhood
of
M
in
N
. Often one identifies the total spaces with their image in
N
, so that the sub-
spaces f(
E
) and f(
D
(x)) are also called tubular neighborhoods of
M
, but the bundle
structure of the subspaces are assumed to be given in any case.
o
Figure 8.34(a) shows an example of a closed tubular neighborhood. The total
space of the closed tubular neighborhood
D
(x) of
M
n
in
N
k
is a k-dimensional differ-
entiable manifold with boundary the total space of the associated sphere bundle
S
(x)).
8.10.12. Theorem.
Every closed submanifold of a closed manifold has a tubular
neighborhood.
Proof.
See [Hirs76].
For more on tubular neighborhoods see [Hirs76]. A related notion is