Graphics Reference
In-Depth Information
that because of Poincaré duality we really only need to assume that the ith homology
groups vanish for 0 < i £ n/2. The hypothesis of the manifold being simply connected
is essential.
Corollary 8.7.6 cannot be strengthened to diffeomorphic because it is known, for
example, that there are seven-dimensional manifolds
M
7
that are homeomorphic but
not
diffeomorphic to
S
7
. The case n = 2 is trivially true, given what we know about
surfaces. The original Poincaré conjecture for dimension 3 is unproved to this day,
although at the time of this writing a proof may finally have been found (see [Miln03],
which also contains a nice overview of the history of the conjecture). The main reason
that the proofs in higher dimensions do not work in dimension 3 is that they rely on
one's ability to deform continuous maps into imbeddings and in three dimensions we
do not have enough space to be able to prove that this can always be done. It should
be noted that an algorithm that determines whether or not a triangulated, closed, ori-
entable three-dimensional manifold is homeomorphic to the 3-sphere
does
exist. See
[Thom98] for a discussion of this algorithm that was discovered by J.H. Rubinstein
in 1992. The proof depends on piecewise linear minimal surface theory. Unfortunately,
it is exponential in the number of tetrahedra and not practically useful, even in the
case of a very small number of tetrahedra.
Finally, we return to the problem of finding minimal cell decompositions for a
manifold. This problem is equivalent to finding a minimal handle decomposition.
Although we know that a manifold admits a handle decomposition, we may not get
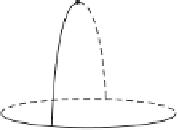
a minimal one. For example, Figure 8.25 shows how the height function applied to
that sphere would produce a handle decomposition for the sphere which has one 0-
handle, one 1-handle, and two 2-handles. The basic idea for finding minimal handle
decompositions is to start with any decomposition and then to simplify it by letting
handles cancel each other. In Figure 8.25, the 1-handle and one of the 2-handles cancel
each other leaving a single 0- and 2-handle, which is a minimal handle decomposi-
tion for the sphere.
8.7.7. Theorem.
(The Minimum Handle Decomposition Theorem) If
M
n
, n > 5, is
a simply connected compact closed differentiable manifold, then there is a nonde-
generate C
•
function f with a minimum number of critical points consistent with the
homology structure. We may assume that the value of the function at its critical points
d
c
b
Figure 8.25.
A nonminimal handle decomposition for
a sphere.
a