Graphics Reference
In-Depth Information
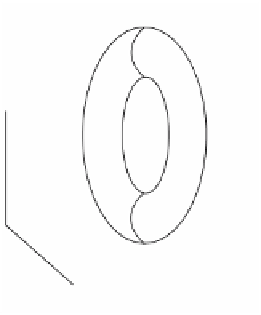
Figure 8.20.
The height function for the torus.
D
z
C
B
y
A
x
In particular, when we talk about
critical points
,
critical values
,
nondegenerate critical
points
, or the
index
of a critical point for functions f :
M
Æ
R
in this section, we shall
mean these concepts as they were defined in Section 4.5 for f
j
. In Exercise 8.6.1 you
are asked to show that everything is well defined and independent of the choice of j.
Now let us return to the subject matter of this section. Let
M
be an n-dimensional
closed manifold and consider a smooth real-valued function f :
M
Æ
R
. Figure 8.20
shows the prototype of the kind of conclusions we want to draw. The figure shows a
vertical torus and the function we have in mind is the height function f, that is,
()
=
f
p
height of
p
above the x
-
y plane
=
z coordinate of
-
p
.
The function f clearly has four critical points at
A
,
B
,
C
, and
D
corresponding to crit-
ical values a, b, c, and d, respectively. Furthermore, these are non-degenerate critical
points because in a neighborhood of these points the manifold looks like the graph
of the functions
(
)
=+
2
2
fxy x y
fxy x y
f
,
,
a
(
)
=-
2
2
,
,
b
2
2
(
)
=-
x y
,
x
+
y
,
and
c
(
)
=-
2
2
fxy
,
x y
-
,
d
respectively. Define
-1
(
-•
]
)
M
s
=
f
,
s
.
How does
M
s
change as the value s changes? Well,
M
s
is the empty set if s < 0. If s is
any number between 0 and a, then
M
s
is diffeomorphic to a disk. When s is between
b and c, then
M
s
is diffeomorphic to a cylinder. When s is between c and d, then
M
s
is like a torus with a disk removed. Finally,
M
s
is the torus if s ≥ d.
There is another way to describe the topological changes in
M
s
. Consider the
difference between
M
b-e
and
M
b+e
. That change is equivalent to adding a “handle” to