Graphics Reference
In-Depth Information
z
z
y
y
x
x
z = x
2
z = x
2
+ y
2
(a)
(b)
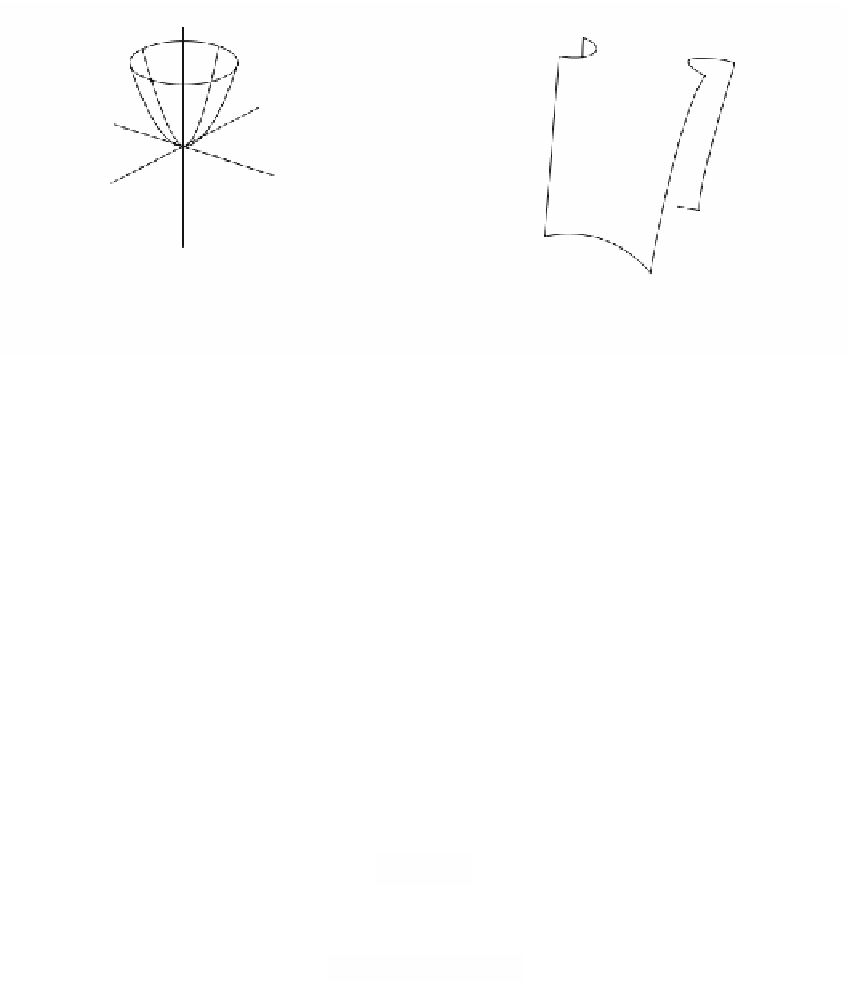
Figure 8.7.
Surfaces that are varieties.
L
P
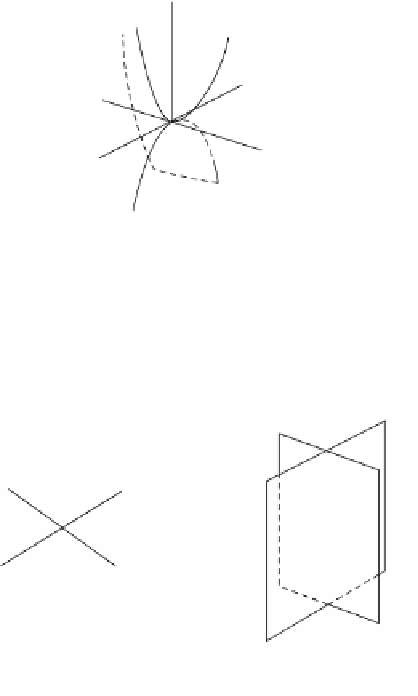
Figure 8.8.
A variety that is not a surface.
(a)
(b)
the polynomial f. It happens that there are some very deep connections between the
two. We shall look at some of this in Chapter 10. The graphs of functions can always
be thought of as varieties. For example, in Figure 8.7 the graph of the functions
(
)
zgxy
=
,
are varieties V(f), where
(
)
=-
(
)
fxyz
,,
z gxy
, .
Not all zero sets V(f) are nice, locally Euclidean spaces. For example, consider the
point
p
in the set in Figure 8.8(a) and the line
L
in the set in Figure 8.8(b). We can
think of these as zero sets of the function x
2
- y
2
in the plane and 3-space, respec-
tively. In the first case we cannot find any neighborhood of
p
that looks like a line. No
matter how small the neighborhood, it will always look like a cross. A similar problem
exists in the second case. It is possible to give examples where worse problems arise.
This leads to the following question: Is there a simple criterion that can be applied to