Algebraic Topology - Computer Graphics and Geometric Modeling - page 441

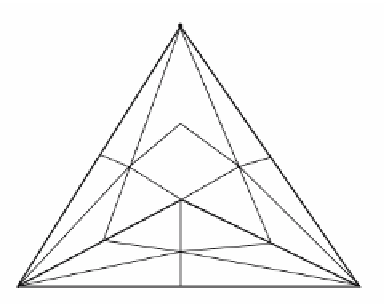
Figure 7.32. Defining the dual cells. C

c

h g

d

b

A

a

e

f

D B

i

subdivision. The dual cell of the 1-simplex AB is the union of the two 1-simplices ab
and af . The dual of the 2-simplex ABC is the 0-simplex b .

The dual cell s n-k will not necessarily be homeomorphic to D n-k . It is if we are
dealing with a proper triangulation for a combinatorial manifold but not for an arbi-
trary pseudomanifold. For example, the dual cell of the vertices p in Figure 7.31 are
not disks. In order for the dual cells to have nice properties we do not need anything
as strong as a combinatorial manifold.

Definition. A closed compact connected topological n-dimensional manifold is
called a homology manifold if it admits a triangulation (K,j) with the property that
the boundary of the star of every vertex in K is a homology (n - 1)-sphere.

Earlier results in this chapter show that the property of being a homology mani-
fold is a topological invariant.

7.5.5. Theorem.

(1) Every homology manifold is a pseudomanifold.
(2) An n-dimensional homology manifold is a manifold when n £ 3.

Proof. See [SeiT80] or [Cair68].

Not every n-dimensional homology manifolds is a manifold when n > 4 (see
[SeiT80] for counterexamples), but they have enough in common to be able to prove
the important duality theorems in Section 7.5.2.
Returning to the dual of a k-simplex s

k

in a simplicial complex K that triangu-

lates a pseudomanifold M n , we have

7.5.6. Proposition .

(1) s n-k is an (n - k)-dimensional pseudomanifold.
(2) If M is a homology manifold, then ∂s n-k is an (n - k - 1)-dimensional homol-
ogy sphere.
(3) The simplex s

k and its dual cell s n-k intersect in the single point b(s).