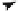Graphics Reference
In-Depth Information
fg
⁄
:
XY Z
⁄
Æ
byfg
⁄
X
=
fandfg
⁄
Y
=
g
.
This map is called the
wedge
of f and g.
With this definition we can now give an alternate definition of the product in
p
n
(
X
,
x
0
). First of all, we can clearly identify maps (
I
n
,∂
I
n
) Æ (
X
,
x
0
) with maps (
S
n
,
e
1
)
Æ (
X
,
x
0
). Let
n n n
:
SSS
c
Æ⁄
(7.9)
be the map that collapses
S
n-1
to the base point of
S
n
⁄
S
n
and that wraps the upper
and lower hemisphere of
S
n
around the first and second factor of
S
n
⁄
S
n
, respectively.
Let [a], [b] Œp
n
(
X
,
x
0
). If we represent a and b as maps
(
)
Æ
(
n
)
a,:
Se
,
Xx
,
,
1
0
then the product [a] * [b] is nothing but the homotopy class of the composite map
(a⁄b)
°
c. See Figure 7.29.
We now have homotopy groups p
n
(
X
,
x
0
) defined for n ≥ 1. It is convenient to make
a definition for n = 0. Note that
S
0
= {-1,+1}.
Definition.
p
0
(
X
,
x
0
) is defined to be the
set
(there is no group structure) of homo-
topy classes of maps
(
)
Æ
(
0
)
f:
S
,
1
X x
,
.
0
(Equivalently, p
0
(
X
,
x
0
) is the set of path components of
X
.)
Although p
0
(
X
,
x
0
) has no group structure, one often refers to it as the 0th homo-
topy “group.”
7.4.3.2. Theorem.
The group p
n
(
X
,
x
0
) is abelian whenever n ≥ 2.
Proof.
Figure 7.30 shows how to construct a homotopy between a*b and b*a.
Just as in the case of the fundamental group, higher homotopy groups are inde-
pendent of the base point if the space is path-connected. One therefore often writes
p
n
(
X
) instead of p
n
(
X
,
x
0
).
S
n
⁄S
n
S
n
a
c
S
n-1
X
b
Figure 7.29.
Using the wedge operation to
define a homotopy group
product.
(a⁄b)
c
°