Algebraic Topology - Computer Graphics and Geometric Modeling - page 425

7.4.2.5. Theorem. The total space of a covering space of a topological manifold is
a topological manifold.

Proof. This is obvious from the local triviality property of the bundle.

When one works with covering spaces or bundles in general, some of the most
important tools are map-lifting tools.

Definition. Let ( Y ,p) be a covering space for a space X and let g : [a,b] Æ X be a con-
tinuous curve. A map ˜ : [a,b] Æ Y is called a lifting of the curve g starting at ˜(a) if
we have a commutative diagram

Y

˜

g Ø p

g

[ ] ææ

ab , X ,

that is, p ° ˜ =g. More generally, given a map f : Z Æ X , any map f: Z Æ Y is called a
lifting of f if we have a commutative diagram

Y

f

p

ææ

Z X ,

that is, p ° ˜ = f.

7.4.2.6. Theorem. (The Path-Lifting Theorem) Let ( Y ,p) be a covering space for a
space X . Let x 0 Œ X and y 0 Œ p -1 ( x 0 ). Then every continuous curve g : [0,1] Æ X lifts
to a unique continuous curve ˜ : [0,1] Æ Y that starts at y 0 .

Proof. We sketch a proof of this theorem. It will give the reader a good idea of the
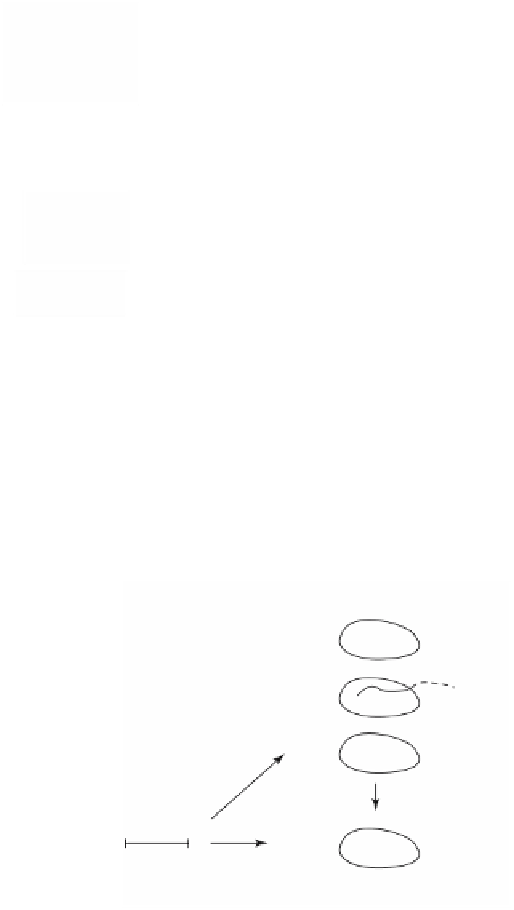
kind of arguments one uses with covering spaces. Figure 7.25 shows what is involved.

p -1 (U)

y 0 Y

~

g

p

g

I

X

g (t)

x 0

0 1 U

Figure 7.25. Lifting paths.