Graphics Reference
In-Depth Information
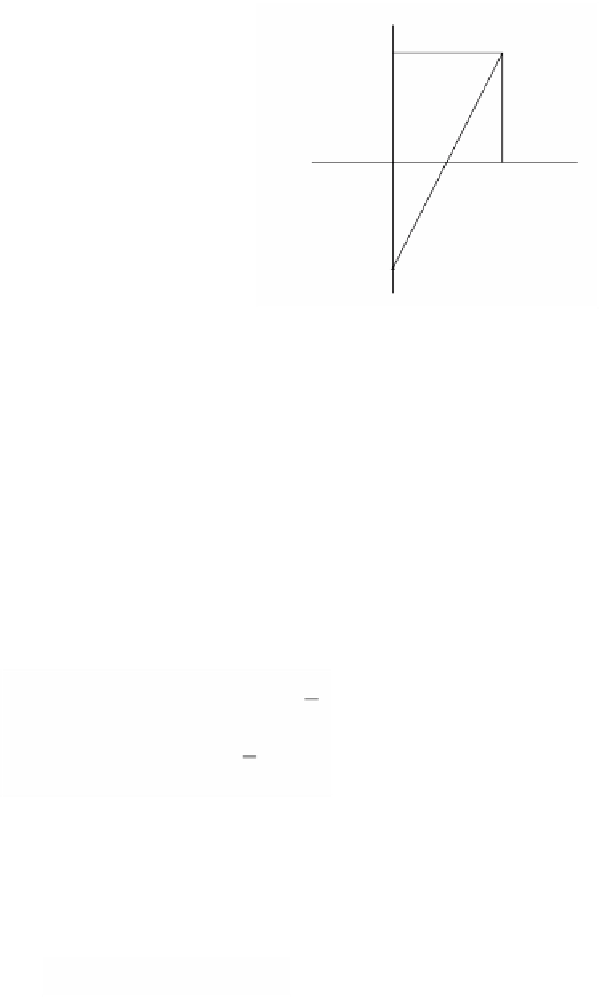
Figure 7.19.
The constant path acts as an identity.
s
a
h
1
h is constant
on these lines
x
0
t
a
c
1
-1
s
h
1
x
0
lines of
constant
value
t
1/2
1
0
a
b
Figure 7.20.
Reverse traversal gives the inverse.
It is easy to check that the map h defined by
1
2
()
=
()
h t s
,
a
2
ts
,
for
0
££
t
,
1
2
(
)
=
a
22
s
-
ts
,
for
££
t
1
,
is a homotopy between a*b and the constant path c. See Figure 7.20. A similar map
shows that b*a is homotopic to c.
Let p
1
(
X
,
x
0
) denote the set of equivalence classes of maps a :(
I
,∂
I
) Æ (
X
,
x
0
) with
respect to the equivalence relation
∂
I
. More precisely,
[
]
(
)
=
(
) (
)
p
Xx
,
I I Xx
,
∂
,
,
.
1
0
0
Define a product * on p
1
(
X
,
x
0
) as follows: If [a], [b] Œp
1
(
X
,
x
0
), then [a] * [b] = [a*b].
7.4.1.5. Theorem.
The operation * on p
1
(
X
,
x
0
) is well defined and makes p
1
(
X
,
x
0
)
into a group.
Proof.
The fact that * is well defined follows from Lemma 7.4.1.1. Lemma 7.4.1.2
shows that * is associative. Lemma 7.4.1.3 shows that if c(t) is the constant path, then