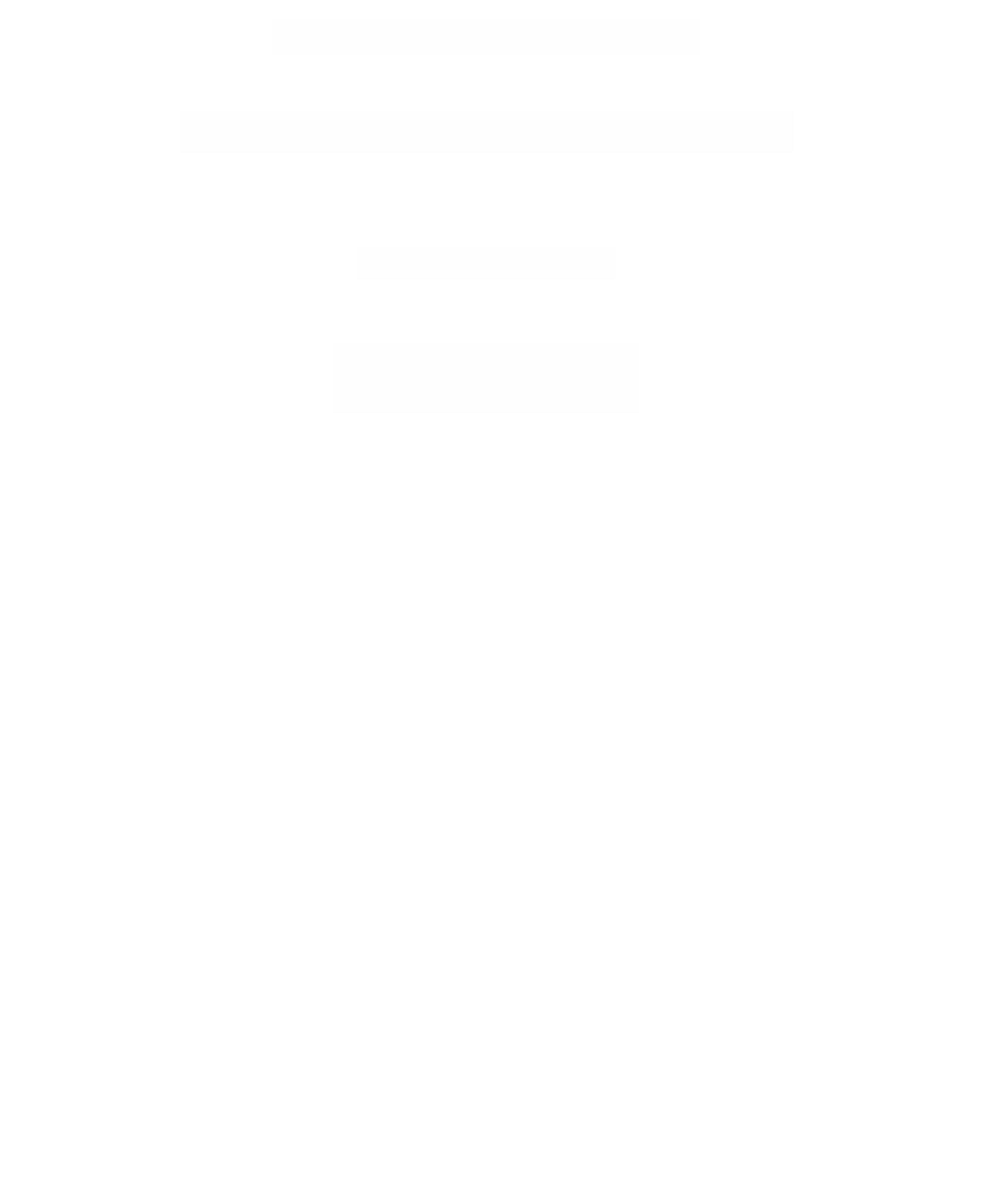Graphics Reference
In-Depth Information
Œ
(
)
vv
+
vv
+
vv vv
,
+
vv
+
vv
CK
;
Z
01
12
20 12
23
31
1
2
and
(
)
+
(
)
=
vv
+
vv
+
vv
vv
+
vv
+
vv
vv
+
vv
+
vv
+
vv
.
(7.5)
01
12
20
12
23
31
01
31
23
20
Recall our intuitive discussion of “holes” in Section 7.2.1. It is what we are doing now
that makes precise the first approach to homology groups in that section.
The boundary map
(
)
Æ
(
)
∂
q
:
CK
;
Z
C
K
;
Z
q
2
q
-
1
2
satisfies
q
Â
(
)
=
ˆ
∂
q
vv
◊◊◊
v
v
◊◊◊
v
◊◊◊
v
,
01
q
0
i
q
i
=
0
that is, ∂
q
sends the boundary of a q-simplex to the sum of all of its (q - 1)-dimen-
sional faces. Proving ∂
q-1
°
∂
q
= 0 is easy in this case because each (q - 2)-dimensional
face a q-simplex belongs to precisely two (q - 1)-dimensional faces of the simplex and
2 = 0 in
Z
2
. The
mod 2 homology groups
of K, H
q
(K;
Z
2
), are now defined to be the
usual quotient group of the kernel of ∂
q
(called the
mod 2 q-cycles
) by the image of
∂
q+1
(called the
mod 2 q-boundaries
).
We can relate the mod 2 q-chains of K to subsets of ΩKΩ.
Definition.
Let c ΠC
q
(K;G). The
support
of c, denoted by ΩcΩ, is the union of all the
q-simplices appearing in c with a nonzero coefficient.
Observe that if we represent q-chains c in C
q
(K;
Z
2
) by the subset ΩcΩ of ΩKΩ, which
is their support, then
(1) The subset Ωc + dΩ is the closure of the symmetric difference ΩcΩDΩdΩ of the
subsets ΩcΩ and ΩdΩ.
(2) The subset Ω∂
q
(c)Ω is the union of all the (q - 1)-simplices that are the face of
an odd number of q-simplices appearing in c.
Now, since
Z
2
is a field, the groups C
q
(K;
Z
2
), Z
q
(K;
Z
2
), B
q
(K;
Z
2
), and H
q
(K;
Z
2
) are
actually vector spaces over
Z
2
.
Definition.
The
qth connectivity number of K
, k
q
(K), is defined to be the dimension
of the vector space H
q
(K;
Z
2
) over
Z
2
. If
X
is a polyhedron, then the
qth connectivity
number of
X
, k
q
(
X
), is defined to be the qth connectivity number of any simplicial
complex K that triangulates
X
.
Connectivity numbers are the mod 2 analogs of Betti numbers. They are well
defined in the case of a polyhedron because the groups H
q
(
X
;
Z
2
) are well defined up
to isomorphism.