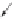Graphics Reference
In-Depth Information
Definition.
Let
L
be an oriented line and let
u
be the unit vector that defines the
orientation of
L
. Let
p
and
q
be two points on
L
. The
oriented
or
signed distance from
p
to
q
, denoted by ||
pq
||, is defined by
pq
=∑.
pq
u
It is easy to check that if
p
π
q
, then ||
pq
|| is just the ordinary (unsigned) distance
|
pq
| if the vector
pq
induces the same orientation on
L
as
u
and -|
pq
| otherwise
(Exercise 1.6.6).
The angle between two vectors as defined in Section 1.3 is always a nonnegative
quantity, but sometimes it is convenient to talk about a signed angle, where the sign
of the angle is determined by the direction (counterclockwise or clockwise) that the
angle “sweeps” out.
Definition.
Let
u
and
v
be two linearly independent vectors in the plane
R
2
. If q is
the angle between
u
and
v
, define -
s
(
u
,
v
), the
signed angle between
u
and
v
, by
-
(
)
=
(
)
2
s
uv
,
q
,
if the ordered basis
uv
,
induces the standard orientation of
R
=-
q
,
otherwise.
This finishes our discussion of the local theory of orientation. We shall return to
the subject of orientation in Chapters 6 and 8 and define what is meant by an orien-
tation at a point of a “curved” space. We shall also consider global aspects of orien-
tation and what it might mean to say that an entire space is oriented. However, in
order not to leave the reader in a kind of limbo with respect to how the definitions of
this section fit into the whole picture, it is useful to give a brief sketch of what is to
come. Surfaces will serve as a good example.
Suppose that
S
is a smooth surface. What we mean by that is that
S
has a nice
tangent plane
T
p
at every point
p
that varies continuously as we move from point to
point. Let us call the point where the tangent plane touches the surface its “origin.”
Since every tangent plane
T
p
is a two-dimensional vector space, we already know what
it would mean to have an orientation s
p
for each
T
p
separately. The family of orien-
tations O = {s
p
} is called an orientation for
S
if the orientations s
p
vary continuously
from point to point. To explain what is meant by the notion of a continuously varying
orientation, note that there is a well-defined one-to-one projection p
p
of a neighbor-
hood of the origin in
T
p
onto a neighborhood of
p
in the surface. Figure 1.14 shows
y = π
q
-1
π
p
(x)
x
T
p
p
q
p
p
p
q
T
q
Figure 1.14.
Defining continuously varying
orientations.