Graphics Reference
In-Depth Information
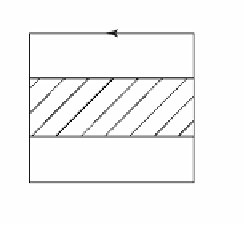
Figure 6.26.
The Klein bottle as the union of two Moebius
strips.
A
2
c
A
1
A
1
d
A
2
sidedness, one could say that if one were to pour water “into” a Klein bottle, then the
water would come right “out,” although this is not quite true since gravity would keep
some of it inside.
Sometimes a Klein bottle is referred to as a sphere with a twisted handle and the
connected sum of k Klein bottles, as a
sphere with k twisted handles
.
6.6
Bordered and Noncompact Surfaces
We finish the chapter with a few comments on “bordered” and noncompact surfaces.
To allow for a boundary we broaden the definition of a combinatorial surface.
Definition.
A
combinatorial surface
(with or without boundary) is a polyhedron
S
that admits a triangulation (K,j) satisfying:
(1) K is a two-dimensional connected simplicial complex.
(2) Each 1-simplex of K is a face of at least one but not more than two 2-
simplices of K.
(3) For every vertex
v
in K, the distinct 2-simplices s
1
, s
2
,..., s
s
of K to which
v
belongs can be ordered in such a way that s
i
, 1 £ i £ s - 1, meets s
i+1
in pre-
cisely one 1-simplex. If s > 1, then s
s
and s
1
have either just
v
or a single 1-
simplex in common.
The
boundary
of
S
, denoted by ∂
S
, is defined to be the set j(Ô∂KÔ). If ∂
S
= f, then
S
is called a
closed
surface. A surface with nonempty boundary is called a
surface with
boundary
or a
bordered surface
.
Clearly, if
S
is a combinatorial surface using the new definition and if ∂
S
= f, then
S
is just a combinatorial surface as defined earlier in Section 6.5. As before, com-
pactness and connectedness is built into the definition of these new surfaces. We shall
again drop the adjective “combinatorial.”
Topologically a bordered surface can be represented by a polygon some, but
not
necessarily all, of whose sides have been identified in pairs. The unidentified sides of
the polygon give rise to the boundary of the surface. Therefore, to classify bordered
surfaces one can take the same approach as the one used to classify closed surfaces.
One shows that every bordered surface can be represented by a labeled polygon and
that such representatives can be put into a “normal form.”