Graphics Reference
In-Depth Information
nected component of the intersection of
S
and a plane through the axis of revolution.
A
circle of latitude
of
S
is a connected component of the intersection of
S
and a plane
orthogonal to the axis of revolution. A
torus
is a surface of revolution where the curve
being revolved is a circle that does not intersect the axis of revolution.
See Figure 1.11. Note that meridians of surfaces of revolution meet their circles
of latitude in a single point. Note also that a surface of revolution may not actually
be a “surface” if the curve being revolved is not chosen carefully, for example, if it
intersects the axis. (The term “surface” will be defined carefully in Chapter 5.) Sur-
faces of revolution are also orientable.
There are surfaces
without
boundary that are nonorientable and the reader is
challenged to find one on his own (or wait until Chapter 6). One word of caution
though: Nonorientable surfaces without boundary cannot be found in
R
3
(see Exer-
cise 6.5.1.). One needs a fourth dimension.
Enough of this intuitive discussion of orientability. Let us move on to mathemat-
ical definitions. In this section we define the most basic concept, namely, what is
meant by the orientation of a vector space. This corresponds to a definition of the
local concept, that is, the notion of an orientation at a point.
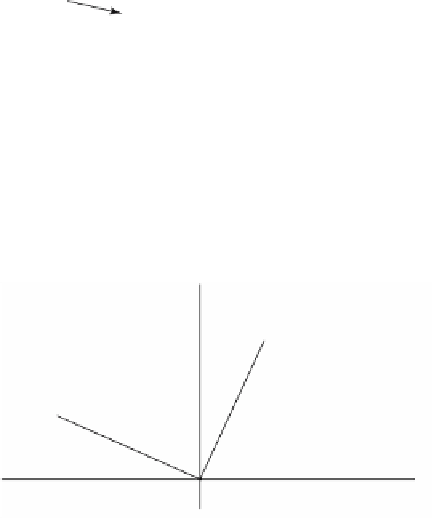
Consider the problem of trying to define an orientation at the origin of
R
2
. Let
(
v
1
,
v
2
) be an ordered basis. See Figure 1.12. We could use this ordered pair to suggest
the idea of counterclockwise motion. The only trouble is that there are many ordered
bases for
R
2
. For example, the pair (
w
1
,
w
2
) in Figure 1.12 also corresponds to coun-
axis of revolution
meridian
circle of latitude
Figure 1.11.
A surface of revolution.
v
2
w
1
w
2
v
1
Figure 1.12.
Using ordered bases to
define an orientation.