Graphics Reference
In-Depth Information
(L,m)
v
0
v
2
v
3
v
0
(L,m)
v
0
v
1
v
2
v
0
v
1
v
4
v
5
v
1
X
(L,m)
≈ S
1
S
1
¥ [0,1]
X
(L,m)
≈
(a)
(b)
(L,m)
v
2
v
1
v
3
v
0
v
2
v
1
X
(L,m)
≈∂
s, where
σ
is a 3-simplex
X
(L,m)
≈ S
2
(c)
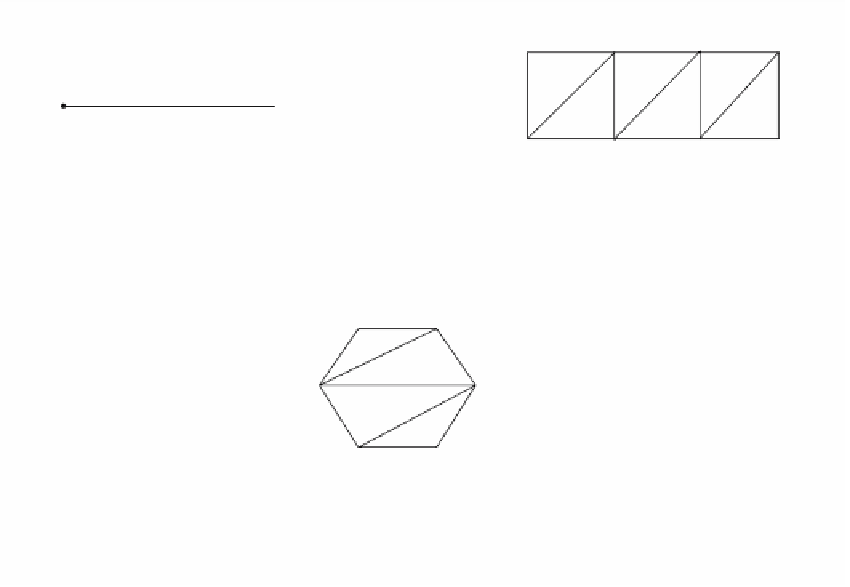
Figure 6.13.
Spaces as labeled figures.
ably the simplest way to describe a space to someone is to do it visually. In practice,
this would mean drawing a picture of it on a flat surface. Consider two-dimensional
spaces such as surfaces. Unfortunately, few of even these special spaces can be flat-
tened out into a plane. Most are also too complicated for an easily understood rep-
resentation by means of projections, but there is another approach. Suppose that we
were able to “cut” the space in a few places and that the result could then be flattened
out. It turns out that as long as we label the resulting flattened figure appropriately
to indicate where the cuts were made, then it will be possible for a person to recon-
struct the space mentally from this labeled figure. As an example of how labeled figures
can describe spaces, consider Figure 6.13. Does the reader see how Figures 6.13 (a)-(c)
are defining a circle, cylinder, and 2-sphere, respectively? Our next task is to make the
passage from a labeled figure to the space it represents rigorous. This is where abstract
complexes come in.
Definition.
A
labeled (simplicial) complex
is a triple (L,m,S), where L is a simplicial
complex, S is a set, and m is a map from the vertices of L to S. The elements of S will
be called
labels
. To simplify the notation, we shall usually drop the explicit reference
to S and talk about the “labeled complex” (L,m) whenever S is clear from the context.
Suppose that (L,m) is a labeled complex. Define an abstract simplicial complex
A
(L,m)
by