Graphics Reference
In-Depth Information
Figure 6.5.
Coloring maps.
B
E
C
D
F
A
G
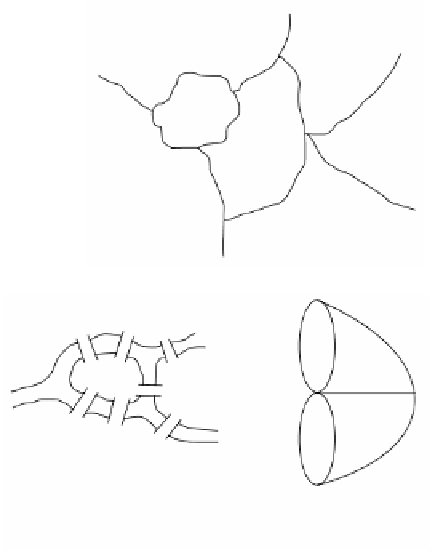
Figure 6.6.
The Königsberg bridges
problem.
(a)
(b)
trefoil knot
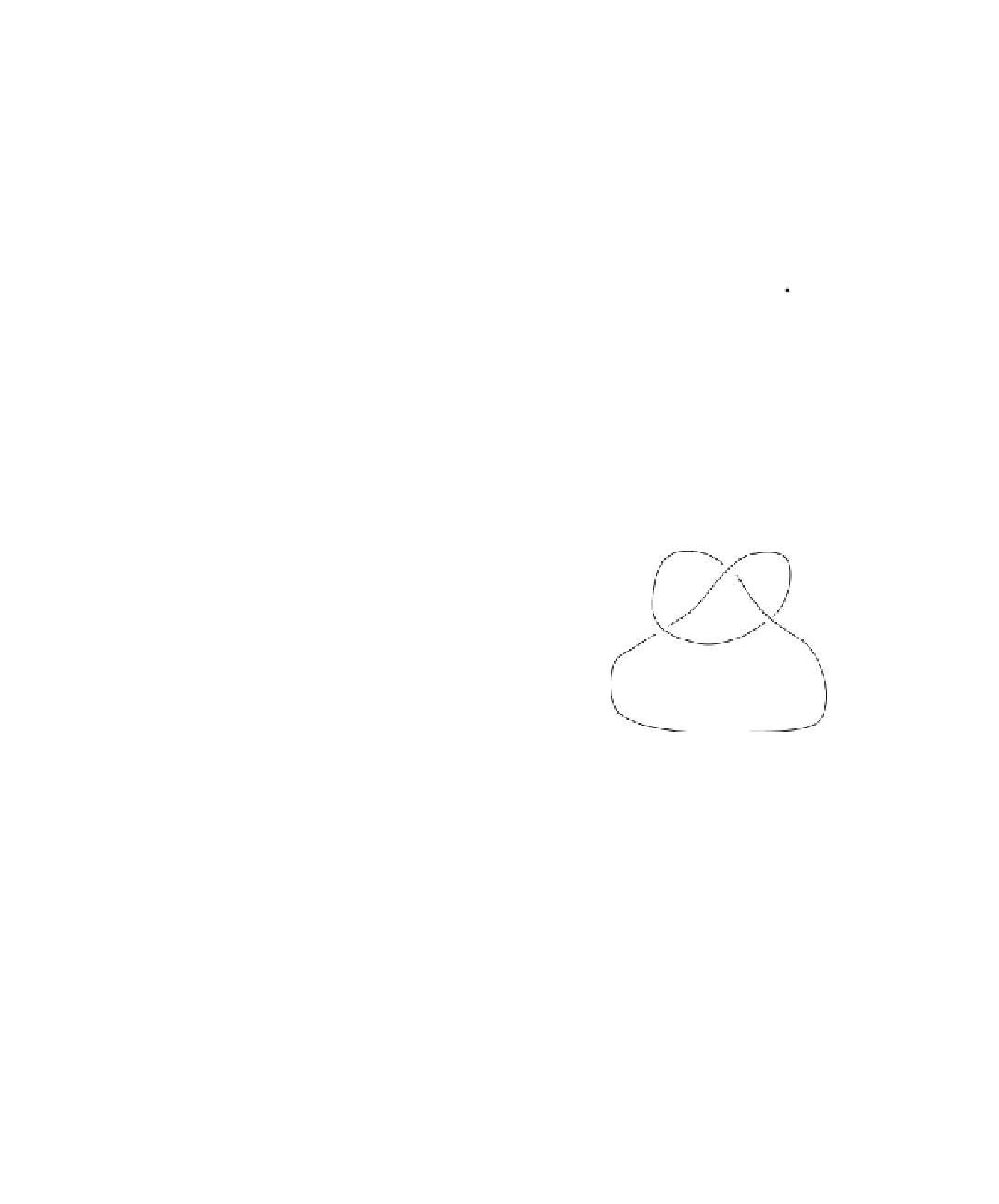
Figure 6.7.
A nontrivial knot.
problem has been generalized to coloring maps on other surfaces such as on a torus.
Interestingly enough, the Euler characteristic, generalized to arbitrary surfaces, shows
up in the formula for the smallest number of colors for such maps.
Graph problems:
A famous example of this type of problem is the Königsberg
bridges problem. The problem was to prove that the seven bridges across the Pregel
river in the Prussian city of Königsberg could not be crossed by walking without
walking across one of the bridges more than once. See Figure 6.6(a). The correspon-
ding graph theory problem, to traverse a graph using each edge exactly one, is shown
in Figure 6.6(b).
Knot theory problems:
Here one wants to classify knots that are thought of as
imbeddings of circles in
R
3
. The unit circle in
R
2
is a trivial knot. An example of a
nontrivial knot is the
trefoil knot
shown in Figure 6.7. One seeks invariants with which