Graphics Reference
In-Depth Information
distance
between
A and B
B
A
distance
between
p and A
A
p
(a)
(b)
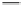
Figure 5.2.
Distances between sets.
The Euclidean metric, the taxicab metric, and the max metric on Euclidean space
are all equivalent.
Definition.
Let (
X
,d) be a metric space. Let
p
X
and
A
X
. Define the
d-distance
from
p
to
A
, dist(
p
,
A
), by
(
)
=
{
(
)
}
dist
pA
,
inf
d
pa a A
,
Œ
.
See Figure 5.2(a). One should think of the distance between a point and a set as
being the “smallest distance” between the point and points of the set. For example,
dist(3,[0,1)) = 2.
Definition.
Let (
X
,d) be a metric space and let
A
,
B
X
. Define the
d-distance from
A
to
B
, dist(
A
,
B
), by
(
)
=
{
(
)
}
dist
AB
,
inf
d
ab a Ab B
,
ŒŒ
,
.
See Figure 5.2(b). One should think of the distance between two sets as being the
“smallest distance” between the points of the sets. For example, dist ([0,1),(3,20]) = 2
and dist ([0,2),(2,3]) = 0.
Definition.
Let (
X
,d) be a metric space. A subset
A
of
X
is said to be
d-bounded
if
there is a constant c > 0 so that d(
p
,
q
) < c for all
p
,
q
A
. If the whole space
X
is d-
bounded, then the metric space (
X
,d) and the metric d are said to be
bounded
. If
A
is
a d-bounded subset of
X
, then the
d-diameter
of
A
, denoted by diam(
A
), is defined by
()
=
{
(
)
}
diam
A
sup
dist
p q
,
p q A
,
Œ
.
For example, the set
X
= (0,1) is a bounded set in
R
, but the set of integers
Z
is
not. The diameter of
X
is 1. The next theorem shows that both a bounded and
unbounded metric on a space can induce the same open sets.
5.2.5. Theorem.
Let (
X
,d) be a metric space. Then
X
admits a bounded metric that
is equivalent to d and for which diam(
X
) £ 1.
Proof.
Define
(
)
=
{
(
)
}
d
*,
pq
min 1
,
d
pq
, .
(5.5)