Graphics Reference
In-Depth Information
4.5.2. Theorem.
Let
X
Õ
R
n
and let f :
X
Æ
R
be a differentiable function. If a point
p
in the interior of
X
is a relative extremum for f, then
p
is a critical point of f.
Proof.
We give a proof for the case where
p
is a local maximum. In that case, f(
q
)
£
p
for all points
q
sufficiently close to
p
. The definition of the directional derivative
implies that D
v
f(
p
) £ 0 for all directions
v
. In particular, D
v
f(
p
) £ 0 and D
-
v
f(
p
) £ 0.
This and Proposition 4.3.18(1) clearly imply that D
v
f(
p
) = 0, so that —f(
p
) =
0
.
Let f : [a,b] Æ
R
be a C
2
4.5.3. Theorem.
function and assume that c in (a,b) is a
critical point of f.
(1) If f≤(c) < 0, then c is a local maximum for f.
(2) If f≤(c) > 0, then c is a local minimum for f.
(3) If f≤(c) = 0, then nothing can be concluded from this test.
Proof.
The easiest way to prove (1) and (2) is to use the Taylor expansion for f. See
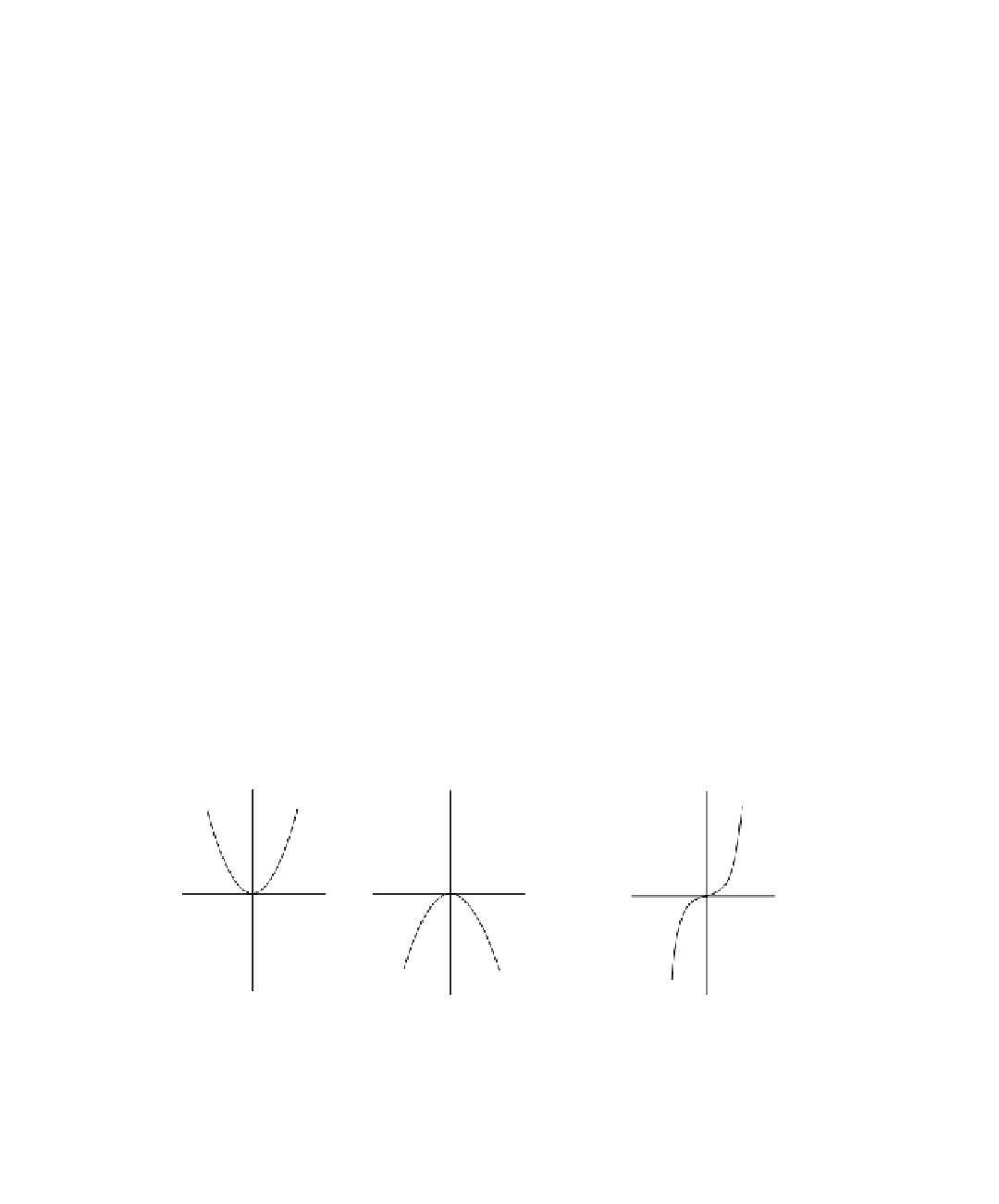
[Buck78]. The canonical examples for (1) and (2) are the functions -x
2
and x
2
, respec-
tively. Their graphs are shown in Figure 4.12(a). To prove (3), simply consider the
functions x
4
, -x
4
, and x
3
(Figure 4.12(b)). This finishes the proof of Theorem 4.5.3.
The graph of the function x
3
shows another property of graphs.
Definition.
A point c is called an
inflection point
of a function f(x) if there is an
e>0, so that either
¢¢
()
<
(
)
¢¢
()
>
(
)
f
x
0
for x
Œ
c
-
e
,
c
and
f
x
0
for x
Œ
c c
,
+
e
or
¢¢
()
>
(
)
¢¢
()
<
(
)
f
x
0
for x
Œ
c
-
e
,
c
and
f
x
0
for x
Œ
c c
,
+
e
.
y
y
y
x
x
x
f(x) = x
2
f(x) = -x
2
f(x) = x
3
(a)
(b)
Figure 4.12.
Some canonical cases of Theorem 4.5.3.