Graphics Reference
In-Depth Information
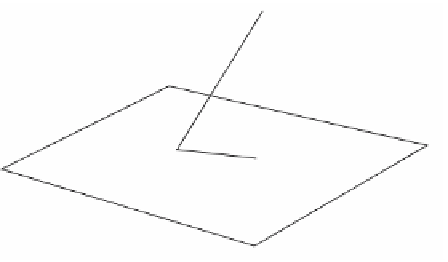
Figure 1.5.
Decomposing a vector with
respect to a subspace.
v
v
^
X
v
ll
Clearly, the orthogonal projection of
v
on
u
is the same as the orthogonal projec-
tion of
v
on the subspace spanned by
u
and hence is really just a special case of the
earlier definition. A similar comment holds for the orthogonal complement. Another
way of looking at what we have established is that, given a subspace
X
, every vector
v
can be decomposed into two parts, one “parallel” to
X
and the other orthogonal to
it. See Figure 1.5.
We finish this section with a look at some very important classes of matrices.
An n ¥ n real matrix A is said to be
orthogonal
if AA
T
= A
T
A = I, that is,
Definition.
the inverse of the matrix is just its transpose.
1.4.7. Lemma.
(1) The transpose of an orthogonal matrix is an orthogonal matrix.
(2) Orthogonal matrices form a group under matrix multiplication.
(3) The determinant of an orthogonal matrix is ±1.
(4) The set of orthogonal matrices with determinant +1 forms a subgroup of the
group of orthogonal matrices.
Proof.
Easy.
Definition.
The group of nonsingular real n ¥ n matrices under matrix multiplica-
tion is called the (real)
linear group
and is denoted by
GL
(n,
R
). The subgroup of
orthogonal n ¥ n matrices is called the
orthogonal group
and is denoted by
O
(n). An
orthogonal matrix that has determinant +1 is called a
special orthogonal matrix
. The
subgroup of
O
(n) of special orthogonal n ¥ n matrices is called the
special orthogonal
group
and is denoted by
SO
(n).
The groups
SO
(n) and
O
(n) play an important role in many areas of mathemat-
ics and much is known about them and their structure. Here are two useful charac-
terizations of orthogonal matrices.
1.4.8. Theorem.
There is a one-to-one correspondence between orthogonal
matrices and orthonormal bases.