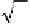Graphics Reference
In-Depth Information
To find D
v
f when
v
= (-1,2) and f(x,y) = x
2
y + e
xy
.
4.3.19. Example.
Since —f (x,y) = (2xy + ye
xy
,x
2
+ xe
xy
), it follows that
Solution.
(
)
∑-
)
(
)
=
xy
2
xy
(
)
=-
xy
2
xy
D
f x y
,
2
xy
+
ye
,
x
+
xe
1 2
,
2
xy
-
ye
+
2
x
+
2
xe
.
(
-
12
,
4.3.20. Example.
To find the directional derivative for
(
)
=
x
F x y
,
e cox y
.
at (0,0) in the direction making an angle of 60 degrees with the x-axis.
). Since —F(x,y) = (e
x
cos y,-e
x
Solution.
The unit direction we want is
v
= (1/2)(1,
3
sin y), it follows that
1
2
3
2
1
2
)
∑=
(
∑
Ê
ˆ
˜
=
(
)
=—
(
DF
00
,
F
00
,
v
10
,
,
.
Á
v
4.3.21. Example.
To find the directional derivative of
(
)
=
23
Fxyz
,,
x yz
along the curve g (u) = (e
-u
,2 sin u + 1,u - cos u) at the point g (0) on the curve.
Solution.
What we are after is the directional derivative of F in the direction of the
unit tangent vector to the curve g (u) at 0. We shall see in Section 8.4 that the tangent
vector
v
(u) to the curve at u can be obtained by differentiating the component func-
tions of the curve, so that
v
(u) = (-e
u
,2 cos u,1+sin u) and
v
(0) = (-1,2,1). Let
u
be
the unit vector in the direction
v
(0). Since —F(x,y,z) = (2xyz
3
,x
2
z
3
,3x
2
yz
2
) and g (0) =
(1,1,-1), our answer is
1
6
3
2
(
)
=—
(
)
∑=--
(
)
∑
(
)
=
DF
11
,,
-
1
F
11
,,
-
1
u
2
,
1 3
,
-
121
, ,
.
u
Here are two more basic theorems for vector-valued functions that extend well-
known results from the case of ordinary functions of one variable.
(The Generalized Mean Value Theorem) Let f :
R
n
Æ
R
m
4.3.22. Theorem.
be a
differentiable function. If
p, q
Œ
R
n
, then
()
-
()
=
()
-
(
)
f
qp
f
f
pqp
*
for some
p
* Π[
p
,
q
].
Proof.
See [Buck78].
The next theorem is a generalization of Taylor's theorem. We shall only state it for
the 2-variable case. First, it is convenient to define a differential operator