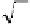Graphics Reference
In-Depth Information
tions by linear functions. In the three examples below, the functions should be thought
of intuitively as parameterizations of certain sets. The derivative will then correspond
to the tangent line or plane at the appropriate points of those sets.
4.3.12. Example.
To find the derivative of p(q) = (cos q,sin q) at q=p/4.
Solution.
By Theorem 4.3.10
-
sin
cos
a
a
Ê
Ë
ˆ
¯
¢
()
=
pa
.
Therefore,
p
4
1
2
1
2
Ê
Ë
ˆ
Ê
Ë
ˆ
¯
()()
=-
(
)
¯
()
=-
Dp a h
h
sin ,
a h
cos
a
and
Dp
h
h
,
h
.
The graph of the function
1
2
1
2
1
2
p
1
2
p
()
=
Ê
Ë
ˆ
¯
+-
Ê
Ë
Ê
Ë
ˆ
¯
Ê
Ë
ˆ
¯
ˆ
¯
Tu
,
u
-
,
u
-
4
4
is in fact the tangent line to the circle at p(p/4).
To find the derivative of f(x,y) = x
2
+ y
2
at (x,y) = (1,0).
4.3.13. Example.
Solution.
By Theorem 4.3.10, f¢(a,b) = (2a,2b). Therefore,
(
)(
)
=+
( ( )
=
Df a b h k
,
,
22
ah
bk
and
Df
,
0
h k
,
2
h
.
The graph of
(
)
=
()
+-
(
)
=-
Txy
,
f
10
,
2
x
1
2
x
1
is the tangent plane to the graph of f at (1,0).
4.3.14. Example.
To find the derivative of f(q,z) = (cos q,sin q,z) at (0,2).
Solution.
By Theorem 4.3.10
-
sin
cos
0
0
01
a
a
Ê
ˆ
¢
(
)
=
Á
Á
˜
˜
fab
,
,
Ë
¯
so that Df(a,b)(h,k) = ((-sin a)h,(cos a)h,k). Clearly, the map