Graphics Reference
In-Depth Information
given that principle, there would have been nothing to prove. The dual of Theorem
3.9.1(2) holds also, again by the principle of duality.
3.10
The Stereographic Projection
The subject matter of this last section is not really part of projective geometry as such
but of geometry in a general sense. The map we shall describe shows up in many
places, including topology and complex analysis. It has many interesting properties
but we shall only take time to discuss those that are relevant to this topic. A good ref-
erence for more information is [HilC99].
Definition.
The
stereographic projection
of the n-sphere
n
-
{
n
p
n
:
Se
Æ
R
n
+1
is defined by
x
x
x
x
x
x
Ê
Ë
ˆ
¯
1
2
n
n
(
)
=
pxx
,
,...,
x
,
,...,
.
n
12
n
+
1
1
-
1
-
1
-
n
+
1
n
+
1
+
1
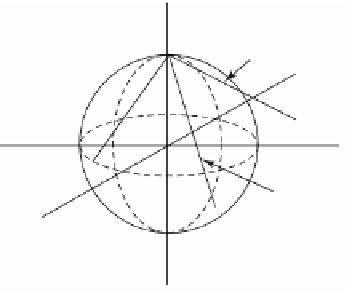
Note that p
n
|
S
n-1
is the identity map on
S
n-1
. The map p
n
can be described geo-
metrically as follows: If
x
Œ
S
n
- {
e
n+1
} and if
L
x
is the ray that starts at
e
n+1
and passes
through
x
, then p
n
(
x
) is the point that is the intersection of
L
x
with
R
n
. See Figure
3.34 for the case n = 2. It is easy to check that p
n
is one-to-one and onto, so that we
may think of
S
n
as
n
•
=»
{}
n
RR
,
where • is the “point of
R
n
at infinity.” Using terminology introduced later in Chapter
5,
S
n
can be thought of as the one-point compactification of
R
n
. The map p
n
extends
to a one-to-one and onto map
e
3
a
S
2
p
2
(a)
p
2
(c) = c
b
p
2
(b)
Figure 3.34.
The stereographic projection.