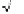Graphics Reference
In-Depth Information
y
Figure 3.17.
Using frames for central
projections.
L
u
2
u
1
p
x
-
1
-
1
.
CFTC TF
=
12
It is easy to check that our answer agrees with the one in Example 3.4.3.1.
3.6
Conic Sections
This section defines the classic conic sections or conics and discusses their geometry.
We analyze the equations that define them and derive the well-known formulas that
are used to classify them. An excellent general reference on the geometry of these
curves is [HilC99]. All our points and sets in this section are assumed to lie in
R
3
.
Definition.
Let
X
be a plane,
C
a circle in
X
, and
p
a point not contained in
X
. The
union of all the lines through
p
and a point of the circle
C
is called a (
circular
)
cone
.
The point
p
is called the
vertex
of the cone. The line through
p
and the center of the
circle
C
is called the
axis
of the cone. If the axis of the cone is orthogonal to
X
, then
the cone is called a
right circular cone
; otherwise it is called an
oblique circular cone
.
Note.
We are using very common terminology here, but we should point out that
the term “cone” is being used here in the sense of a “cone of lines.” In other contexts
like topology a more accurate term for what we are calling a “cone” would be “double
cone.” See Section 5.4.
Definition.
A
conic section
is any set of points obtained as the intersection of a cir-
cular cone and a plane. It the plane passes through the vertex of the cone, then the
conic section is called
degenerate
; if not, the conic section is called
nondegenerate
.
See Figure 3.18 for examples of some conic sections. The next theorem is helpful
in deriving an analytic version of the definition of a conic section.
3.6.1. Theorem.
Every nondegenerate conic section is a set of points in a plane that
is either a circle with positive radius or a set with the property that the ratio e of the