Graphics Reference
In-Depth Information
rotation, reflection
shearing, local scaling
perspective
a
11
a
12
a
13
a
14
a
21
a
22
a
23
a
24
a
34
a
31
a
32
a
33
a
41
a
42
a
43
a
44
translation
global scaling
The above matrix for a projective transformation is not unique. One can always mul-
tiply each entry by a fixed nonzero constant and the resultant matrix will also repre-
sent the same transformation.
As before, there is one matrix that is of particular interest. Consider the matrix
1000
0100
000
0001
Ê
ˆ
Á
Á
Á
˜
˜
˜
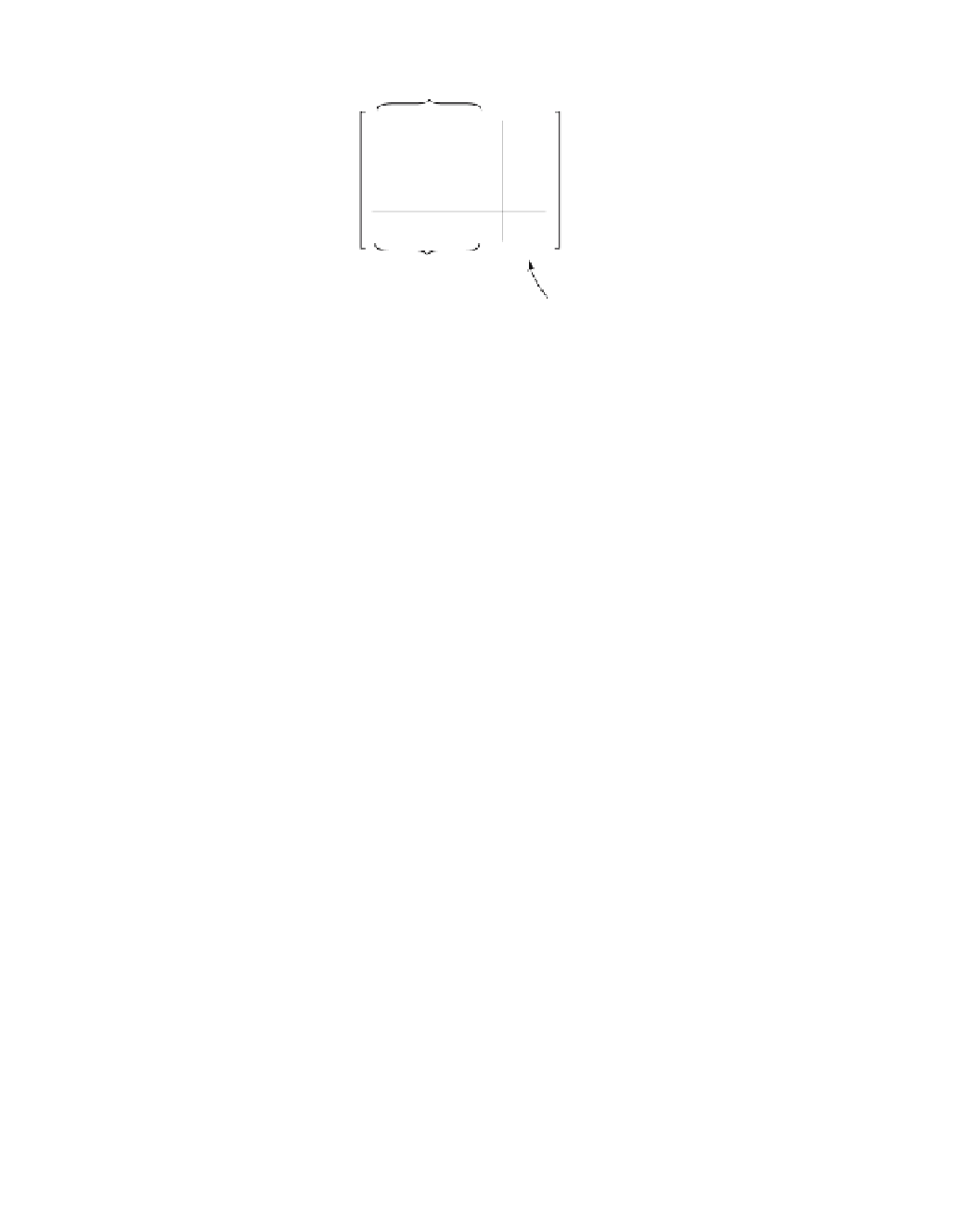
M
a
=
.
a
Ë
¯
This matrix represents a map C
a
:
R
3
Æ
R
2
that is the central projection of
R
3
onto
the x-y plane from the point (0,0,-1/a) on the z-axis (the analog of the planar map C
a
in Section 3.4.3). To see this, note that
[
]
[
]
.
xyz M
1
=
xy
0
az
+
1
a
In other words,
x
az
y
az
Ê
Ë
ˆ
¯
(
)
=
Cxyz
,,
,
,
a
+
1
+
1
which agrees with what this particular central projection should do.
3.5.1.1. Example.
Find the central projection S of
R
3
from the origin onto the plane
X
defined by the equation 2x - y + z = 6.
Solution.
We shall solve this problem in three different ways. The first and most
trivial solution is simply to find the intersection of lines through the origin with the
plane
X
. Now the parametric equation of the line
L
through the origin and the point
(x,y,z) are